Surfaces studied by Lagrange in 1760, Meusnier in 1776, Monge in 1784, Legendre in 1787, Scherk in 1835, Weierstrass in 1866 etc... Websites:  Wikipedia Classical Minimal Surfaces in Euclidean Space by Examples Slide show with a lot of examples Lecture notes by Meeks and Perez virtualmathmuseum.org/Surface/gallery_m.html www.ugr.es

 

Partial differential equation: , i.e.  (see the notations). Weierstrass parametrization: , with , where f is a meromorphic function and g a holomorphic function. First fundamental quadratic form in the case  : .

A minimal surface is a surface each point of which has a neighborhood that is a surface of minimal area among the surfaces with the same boundary as the boundary of the neighborhood. A necessary and sufficient condition is that the mean curvature is equal to zero at all the points, in other words that the principal radii of curvature are opposite of one another at all the points, or also that the Dupin indicatrix is a rectangular hyperbola; except in the case of the plan, all of its points are therefore hyperbolic; the asymptotic lines form a double lattice of orthogonal curves, and the curvature lines are their perpendicular bisectors.

This condition of zero mean curvature means that the curvature energy is equal to zero and thus that the stability of these surfaces is maximal; it is physically produced by a thin layer of soap subject to equal pressure on each side (when the pressures are different, we get the surfaces with constant mean curvature).

Any surface with minimal area supported on one or several bounded curves is minimal in the above sense. The converse is false: for example, a portion of right helicoid between two segment of parallel lines is a minimal surface but its area is greater than that of a portion of a plane.

The Plateau theorem (after Joseph Plateau (1801 - 1883): Belgian physicist, but the theorem was proved only in 1931 by Douglas and Rado) states that there always exists a minimal surface the boundary of which is a given closed bounded contour with no self-intersection and untied (and this surface plus its boundary is homeomorphic to the disk plus its boundary); moreover, these surfaces are in finite number, do not intersect, and one of them has the minimum area among all the surfaces supported on this contour.

The Björling theorem states that there exists an analytical minimal surface with given geodesic (this surface is unique if the value of the normal vector along the curve is set).

The straight line is the shortest path between two points, but we will see that, on the contrary, a surface composed of straight lines (i.e. a ruled surface) is rarely minimal...
 
 

Examples	Weierstrass parametrization
- the catenoid (1740), only non planar surface of revolution to be minimal, Björling surface associated to a circle.	or
- the right helicoid (1776) only non planar ruled surface to be minimal.	or
- the minimal helicoids (1835), including the two previous surfaces, Björling surfaces associated to a circular helix.	or
- the Scherk surfaces (1835), the first one being the only translation surface to be minimal.
- Catalan's minimal surface (1855), Björling surface associated to a cycloid.
- Henneberg's surface (1858), Björling surface associated to a cubical parabola.
- the Bour surface (1861).
- the Enneper surface (1863), Björling surface associated to a Tschirnhausen cubic and Plateau surface associated to the seam line of a tennis ball.
- the family of Enneper surfaces that includes the last 2 surfaces.
- Jeener's flower
- the family of Richmond surfaces.	, or
- the skew catenoid or Riemann minimal surface, only circled surface to be minimal (1860).	elliptic functions
- the Riemann finite minimal surface (198..)
- Meeks' minimal Möbius strip (1981).
- Costa's surface (1982)
- the trinoid and the n-noids (1983)
- the triperiodic minimal surfaces: Schwarz surfaces (1864), Neovius surface (1883), gyroid (1970)

 
 

If we take  , or , then we get the surface parametrized by which has, apparently, not been studied but is not less interesting than the previous ones... It is, in particular, simply periodic. The view on the right shows the coordinate lines; the projections on a horizontal plane of the lines with constant u are trochoids.

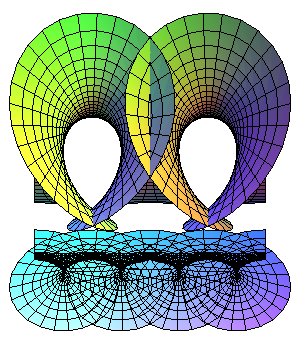If we take , then we get the parametrization  of a surface named by Patrice Jeener "wave minimal surface".

Björling surface associated to a parabola:

Björling surface associated to a sinusoid:

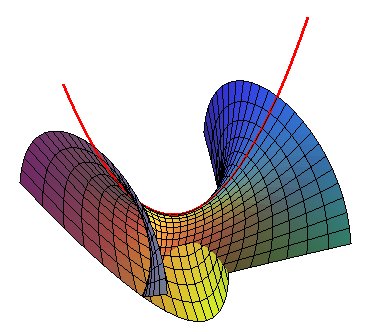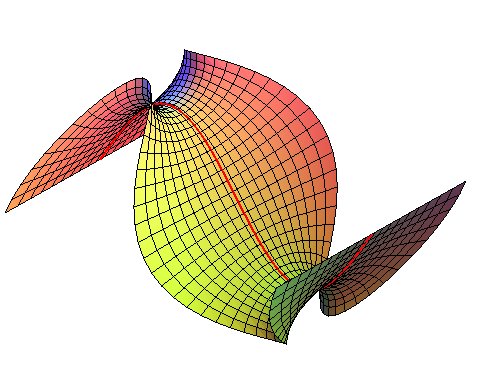Björling surface associated to a lemniscate of Gerono.

 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL   2017