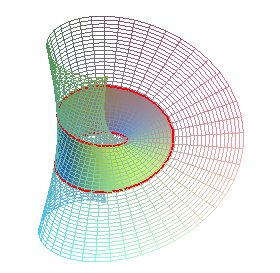
MÖBIUS SURFACE
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
MÖBIUS SURFACE
| See the "exam papers" X 1977 math 2 and agreg 1929. |
Cartesian parametrization:  .
Toroidal equation:  .
Cylindrical equation:  .
Cartesian equation: 
, i.e. , simplifying by y, 
or also  .
Ruled cubic surface. Gaussian curvature:  .
Self-intersection line: x = -a ; y = z ; axis of symmetry Ox. Directrix cone with directrix 
which is a clelia with
parameter n = 1/2. |
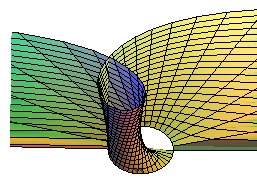
The Möbius surface or half-twist surface is the non-developable ruled surface generated by the rotation of a line on a plane turning on itself around one of its lines with an angular speed equal to twice that of the line; it is therefore a special case of rotoid.
The Möbius surface is called this way because its
portion obtained for 
with 
is
a Möbius strip.
It can also be defined as the ruled surface the directrices
of which are a circle (here, 
),
the axis of this circle (here, Oz) and a line forming an angle of
45° with respect to the plane of the circle, the projection of which
is a line tangent of the circle (here, x = -a , y = z ). Since it
has two linear directrices, it is a conoidal
surface.
 |
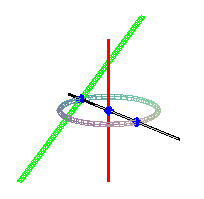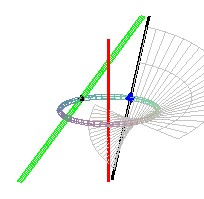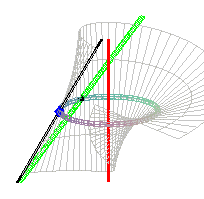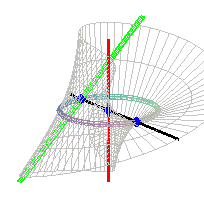The respective intersection points between the generatrix
and the circle, the red axis, and the green line, are  . |
Besides, the Möbius surface is projectively equivalent
to Zindler's conoid; indeed
the change 
transforms the homogeneous equation 
of the Möbius surface into the equation 
of this conoid.
The sections by the horizontal planes z = b
are strophoids,
with equation  . |
 |
| The section by the sphere with center O and radius R is composed of a Viviani curve and of the equator of the sphere. |  |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018