| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RECIPROCAL POLAR OF A SURFACE
1) Some reminders on poles and polars.
Two points M and M0 are said to be conjugates with respect to a sphere (S) with center O and radius a when the sphere with diameter [M0M] is orthogonal to (S), which translates into ; this comes from the fact that when the line (M0M) cuts the sphere at A and B, M and M0 are harmonic conjugates of one another with respect to [AB].
The polar plane of a point M0 with respect to (S) is then the locus of the conjugates M of the point M0 with respect to the sphere, and is therefore defined by ; it is the perpendicular plane of the line (OM0) passing by the inverse of M0 with respect to (S); it is also the radical axis of the sphere (S) and of the sphere with diameter [OM0].
When M0 is outside of
(S), it is the plane of the circle of the contact points between the tangents passing by M0 and the sphere
(S). Inversely, a plane is the polar plane of a unique point, called its pole.
Though it is related to the inversion, the natural space of this transform is not the conformal 3D space, but the projective 3D space: the polar plane of the point O is the the plane at infinity, and the polar plane of a point at infinity is the plane passing through O perpendicular to the direction of the point.
2) Definition of the reciprocal polar of a surface with respect to a sphere.
The reciprocal polar of a surface (S0) with respect to a sphere (S) (or with directrix sphere (S)) is the envelope of the polar planes of the points on (S0) with respect to (S); it can be proved that it is also the set of all the poles of the tangent planes of (S0) with respect to (S).
This transform, called reciprocal polar transform, is an involution, in other words, the reciprocal polar of the reciprocal polar is equal to the initial curve.
The inverse of the reciprocal polar with respect to the same sphere is none other than the pedal surface of the initial surface; this can be summarized by the following diagram:
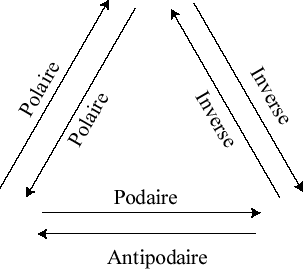
The reciprocal polar of an algebraic surface is an algebraic surface the degree of which is equal to the class of the initial curve (i.e. to the degree of the tangential equation).
3) Definition of the polar developable of a curve with respect to a sphere.
The polar developable of a curve (G0) with respect to a sphere (S) (or with directrix sphere (S)) is the envelope of the polar planes of the points of (G0) with respect to (S); it can be proved that it is also the set of all the poles of the osculating planes of (G0) with respect to (S).
Do not mistake with notion for that of polar developable of a curve, generated by the polar lines.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017