PSEUDOSPHERE
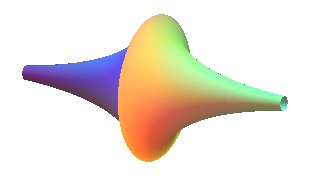
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PSEUDOSPHERE
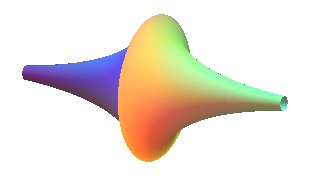
| Surface studied by Ferdinand Minding (1806-1885) and
Eugene Beltrami in 1868, the latter named it pseudosphere.
Other names: Beltrami surface, tractroid, tractricoid. |
| Cartesian parametrization: or where Parametrization for which the coordinate lines are the asymptotic lines: With the first parametrization: First fundamental quadratic form: Constant total curvature: Equation of the geodesics: Volume: |
The pseudosphere is the surface of revolution generated
by the rotation of a tractrix
around its asymptote.
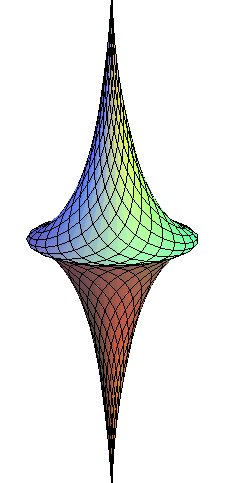
It is called this way because its Gaussian
curvature is constant, like that of the sphere, but negative (it is
not the only surface of revolution that has a constant negative Gaussian
curvature, see the other ones here).
Beltrami considered this surface because it constitutes
a model of the hyperbolic plane.
Indeed, by a given point, there pass an infinite number
of "parallel" geodesics, i.e. that do not meet a given geodesic.
 |
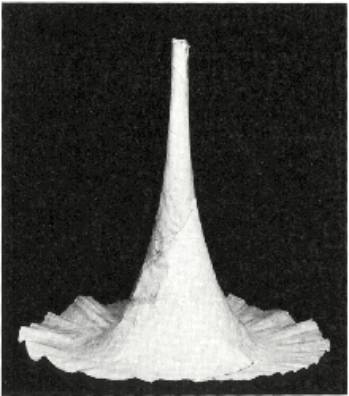
Original model of the pseudosphere constructed by Beltrami. |
See also the pseudospherical
helicoid, which is a generalization.
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017