Quadric

QUADRIC

From the Latin quadrus: square.

A quadric is an algebraic surface of degree 2; see the classification below.

Cartesian equation: , where P is a polynomial of degree 2.
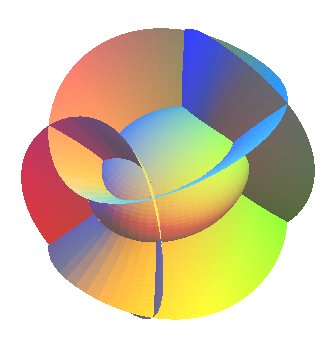
The quadric is said to be non degenerate if the homogeneous quadratic form is non degenerate, i.e. of rank 4 (which amounts to saying that the surface is smooth).
When the rank of this form is equal to 3, we get the cones and cylinders of second degree, and when it is less than or equal to 2, the quadric is the union of two planes.
Reduced Cartesian equation (up to isometry) of the quadrics: with .
I) Real affine classification.
Up to an affine transformation, there are 9 - non empty, not decomposed, and not reduced to a point- real cases, 5 non degenerate cases and 4 of rank 3:
1) The three are nonzero and have the same sign: ellipsoid with reduced equation .
2), 3) and 4) The three are nonzero but do not have the same sign: one- or two-sheeted hyperboloid or elliptic cone (of rank 3) with respective reduced equations .
5), 6) One of the is equal to zero, the other two have the same sign: elliptic paraboloid: or elliptic cylinder (of rank 3): .
7), 8) One of the is equal to zero, the other two have opposite signs: hyperbolic paraboloid: or parabolic cylinder (of rank 3): .
9) Two of the are equal to zero, the other one is not: parabolic cylinder (of rank 3): .
II) Real projective classification.
There remain only two non-empty types:

ellipsoid,
elliptic paraboloid,
two-sheeted hyperboloid:
non degenerate quadrics with elliptic points

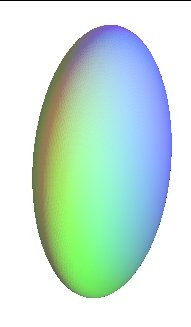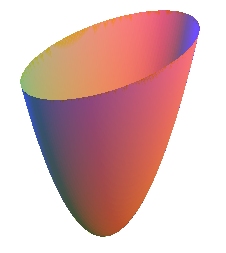
Up to homography, these 3 quadrics are identical!

and
one-sheeted hyperboloid
hyperbolic paraboloid:
non degenerate ruled quadrics (with hyperbolic points)

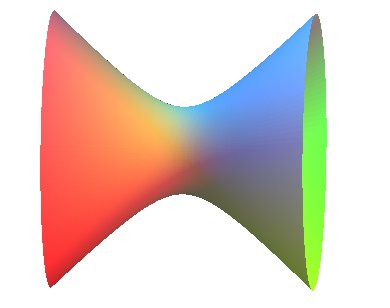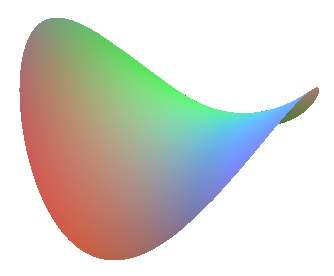
Ditto.

and one non-empty type of rank 3: .
III) Complex projective classification:
One non-degenerate type: and one type of rank 3: .

Homofocal quadrics and triple orthogonal system of non-degenerate quadrics.
If a > b > c, then the quadrics with equation are non-degenerate quadrics the sections by the symmetry planes of which are confocal conics (i.e. with the same focus); the 6 foci are , , .
For we get a first family, composed of ellipsoids, for we get a second family, composed of one-sheeted hyperboloids, for , we get a third family, composed of two-sheeted hyperboloids.
Moreover, these three families form a triple orthogonal system, which means that any surface of each family intersects perpendicularly any surface of the other two families.
The intersection lines are curvature lines (Dupin theorem).
Opposite, an example of each family; to know which one is the two-sheeted hyperboloid, look at: .

Contrary to the plane case, the equation , where F(a, 0, 0) is a point and H the projection of M on a line (D) = Oz does not give all the quadrics. The reduced equation being , we obtain an ellipsoid of revolution for k < 1, a parabolic cylinder for k = 1, and a hyperboloid of revolution for k > 1 (opposite).

next surface previous surface 2D curves 3D curves surfaces fractals polyhedra