Surfaces studied by Schwarz in 1864, then by A. H. Schoen in 1970, who gave the abbreviations "P" and "D". Hermann Amandus Schwarz (1843-1921): German mathematician. Websites: Wikipedia Povray views of this page made by Alain Esculier

 

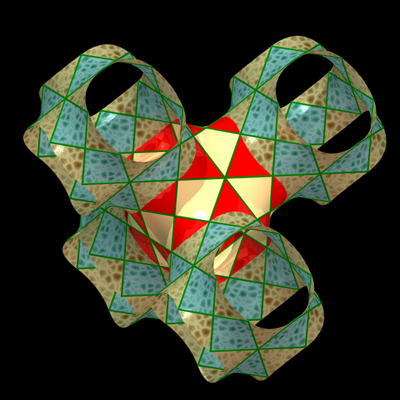
The Schwarz "D" (for diamond) minimal surface is the triply periodic minimal surface the fundamental patch of which is the solution of the Plateau problem for a contour that is one of the 6 skew quadrilaterals made from a skew hexagon inscribed in the edges of a cube, as represented opposite. The Schwarz "P" (for primitive) minimal surface is the surface built similarly to the previous one from a skew hexagon this time inscribed in the edges of a regular octahedron.

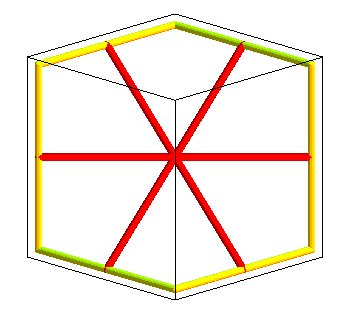Skew hexagon, base of the Schwarz D surface, composed of 6 skew quadrilaterals; the yellow edges are 6 of the 12 edges of a cube. Each Plateau quadrilateral has 3 right angles, an angle of 60°, and two sides equal to sqrt(2) times the other two.

Skew hexagon, base of the Schwarz P surface, composed of 6 skew quadrilaterals; the yellow edges are 6 of the 12 edges of a regular octahedron. Each Plateau quadrilateral has 2 right angles and 2 angles of 60°, and 4 equal sides.

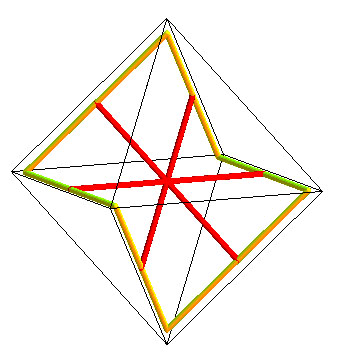The Plateau solution for a skew quadrilateral is not, like it could be hastily thought, a portion of hyperbolic paraboloid (HP) the generatrices of which are its sides, and one will find, here for Schwarz D, and here for Schwarz P, the exact calculation of this solution (and one will find in these articles that the two surfaces are conjugated by the Bonnet transform): the Weierstrass parametrization is obtained with ,  for D and  for P. In the opposite views of the 6 surfaces supported on the 6 skew quadrilaterals, we used a triangulation method that provides a surface supported on the considered contour, but which is not the Plateau surface; the method is detailed at the bottom of this page.

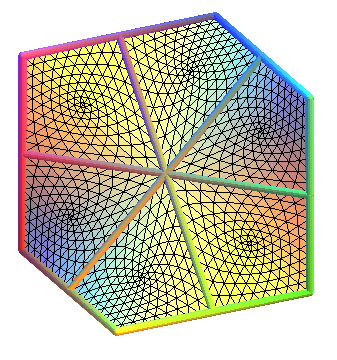
Base hexagon for Schwarz D

Base hexagon for Schwarz P

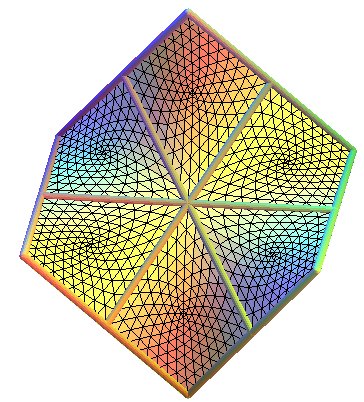
The complete Schwarz D surface is obtained by applying the 6 symmetries with respect to the 6 sides of the base hexagon and iterating to infinity.		The complete surface is obtained by translations of this composition of 4 base hexagons.
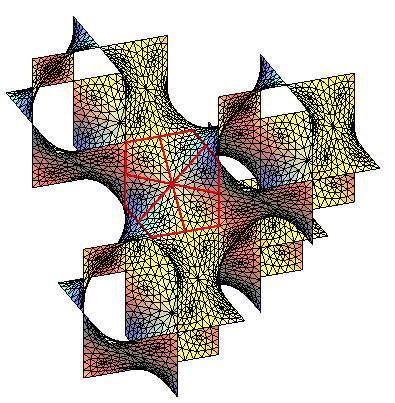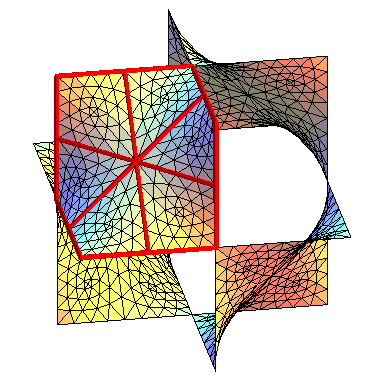Ditto for the P surface.		The complete surface is obtained by translation of this composition of 12 base quadrilaterals. Note that the surface is minimal but is not a surface with minimal area among the surfaces supported on the upper and lower squares...

 

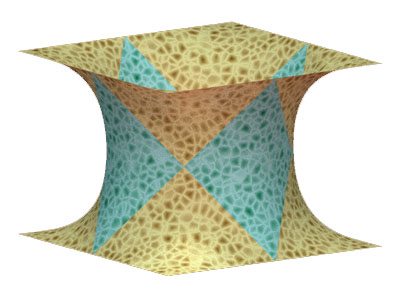The complete P surface can be seen as a network of pipes crossing at right angles (hence the nickname of "plumber's nightmare").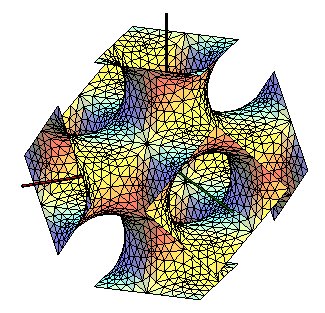

Pattern composed of 26 fundamental quadrilaterals.  By replacing the Plateau quadrilaterals by portions of hyperbolic paraboloids, we get the sculpture by Angel Duarte in Lausanne.

If half of the 24 quadrilaterals of the previous pattern are carved out, we get a pattern that generates the entire surface by translations.

This concrete construction shows how the complete sphere is built based on the previous pattern, and also shows that the surface splits the space into two connected parts that can be superimposed (the inside of the pipes is isometric to the outside).

 

The complete D surface can be seen as a network of pipes crossing at angles of 109°28', like the segments joining the center of a regular tetrahedron to the 4 vertices. Here also, the inside and the outside of the pipes can be superimposed.
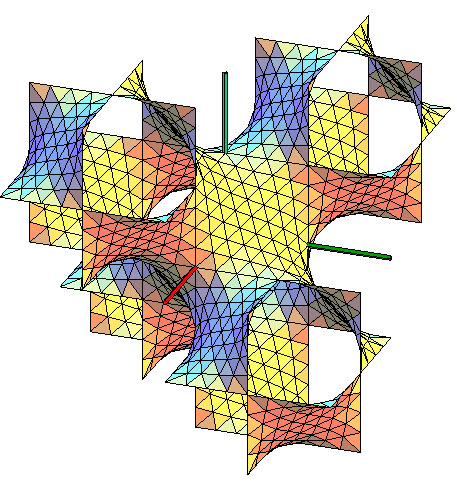Another way of constructing the final D surface is to begin by making this saddle composed of 4 base hexagons, and then to duplicate it by translations:

 

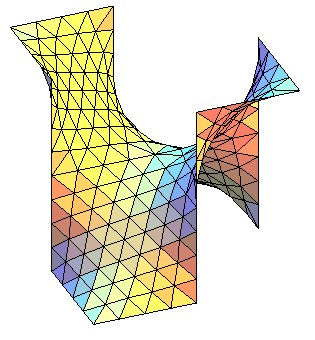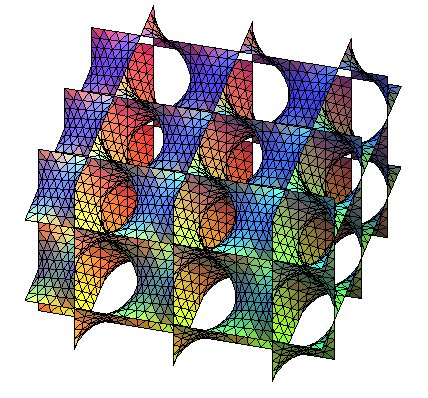The D and P surfaces can be approximated by so-called "nodal" surface with respective Cartesian equations: and , they are also triply periodic, but not minimal.

Approximate D surface res:=90:maxi:=5*Pi/2:f:=(x,y,z)->if x+y+z<maxi and x-y-z<maxi  and -x+y-z<maxi and -x-y+z <maxi then cos(x)*cos(y)*cos(z) -sin(x)*sin(y)*sin(z) else NULL fi:   implicitplot3d(  'f'(x,y,z), x=-maxi..maxi ,y=-maxi..maxi, z=-maxi..maxi,grid=[res,res,res],style=patchnogrid,lightmodel=light2,scaling=constrained,orientation=[140,25]);

Approximate P surface

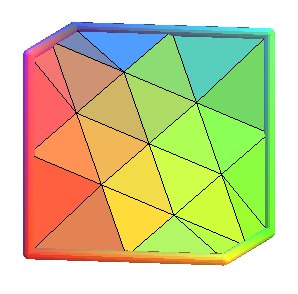
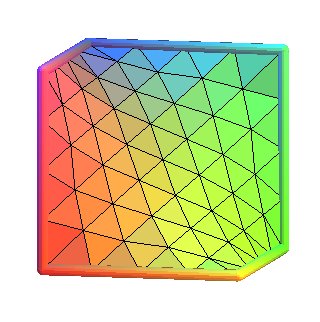
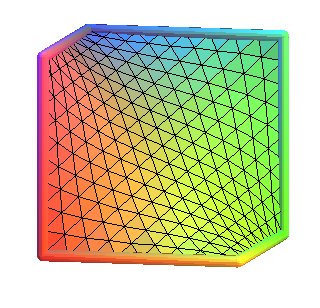
Explanation of the process of triangulation above, not on a quadrilateral, but directly on the skew hexagon of the D surface:
We start from the 6 triangles delimited by the 3 diagonals of the contour; then for each triangle, define 3 points "corresponding" a bit to each middle of the sides, with 2 cases:
If the side is on the contour: then the point really is the middle of this side.
If the side is not on the contour: then the point is the barycenter of the vertices of the faces that have this side in common (therefore the ends of the common side count twice).
The triangle is then split into 4 smaller triangles, the vertices of which are those of the initial triangle plus the 3 points defined.
Here are the 5 first steps of this process, the fifth traced without the triangles:

See also the Neovius surface and the gyroid, minimal surfaces that have the same Weierstrass representation as the D and P surfaces, but another Bonnet angle.

Schwarz D

Schwarz P

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  Alain ESCULIER 2017