In the most general meaning, a surface with rotational symmetry is a surface invariant under the action of a symmetry of a nonzero angle.
A surface is said to have rotational symmetry of order n if it is invariant under the action of a rotation by an n-th of a turn (and not invariant by a rotation of a smaller angle).
A surface with rotational symmetry of order n might not have a plane of symmetry (see for example the Klein bottles of order n), but the surfaces with rotational symmetry of order n that have a plane of symmetry are the surfaces that have exactly n planes of symmetry that pass through one axis. Then, they have (at least) the symmetries of a regular pyramid with n lateral faces.

It is the generalization to space of the notion of curve with rotational symmetry (and all the sections by planes perpendicular to the axis of rotation are such curves).
 
 

General cylindrical equation of a surface with rotational symmetry of order a multiple of n:	Corresponding Cartesian equation:
with f of smallest period with respect to equal to ,	with
Special case:  (has n planes of symmetry)	with

The case n = 2 is studied at flippable surface (surface invariant under the action of a half-turn).
Any cylinder or right cone with directrix a curve with rotational symmetry is a surface with rotational symmetry.

Examples of families of algebraic surfaces with rotational symmetry:
 

Name	Polar equation	Cartesian equation	n = 2	n = 3	n = 4
Plücker's conoid		algebraic surface of degree n+1 for n even,  of degree 2n +2 for n odd		remark: the symmetry is of order 6
Octopus saddle		algebraic surface of degree n	horse saddle	monkey saddle
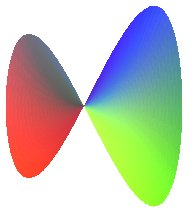
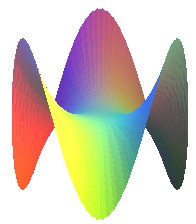
Sinusoidal cone		algebraic surface of degree n for n odd,  of degree 2n for n even	remark: symmetry of order 4		remark: symmetry of order 8
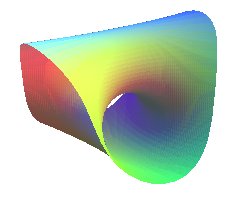
??		algebraic surface of degree n+1 for n even, of degree 2n +2 for n odd	parabolic cyclide
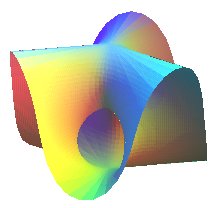Costa's algebraic surface		algebraic surface of degree n+1 for n even, of degree 2n +2 for n odd

 
 

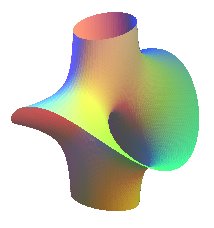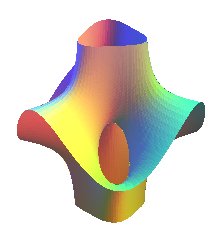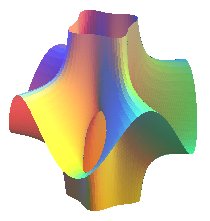Regarding the parametrized surfaces, we get a large family of surfaces with rotational symmetry of order n by taking  where f is a complex function - periodic with respect to its first variable, and g, as well, but real. For example, for , we get the opposite surface, in which appears a trapezohedron. Morin's surface of order n is also such a surface.

Several families of minimal surfaces have rotational symmetry of order n:

the Enneper surfaces, the Richmond surfaces, the n-noids, and the Costa-Hoffman-Meeks surfaces.

For other surfaces with symmetries, see Goursat surface.

Surface with rotational symmetry of order 5, by Patrice Jeener, with his kind authorization

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017