Les droites
Ceci utilise le fait que si 3 droites sont deux à deux non coplanaires, il passe par ces 3 droites une unique quadrique propre qui est la réunion des sécantes communes à ces 3 droites, et que toute quadrique propre réglée (ce qui est le cas de toute quadrique en géométrie complexe, et le cas du paraboloïde hyperbolique ou de l'hyperboloïde à une nappe en géométrie réelle) possède deux familles de génératrices telle que toute droite de la première famille est sécante à toute droite de la deuxième.
Supposons donc qu'il existe un double-sept
tel que deux droites sont sécantes ssi elles ne sont ni dans la
même colonne, ni dans la même ligne.
Les droites
engendrent une quadrique propre réglée (Q) qui contient
leurs sécantes communes
; mais
est une sécante commune à
, qui engendrent la même quadrique (Q) :
fait donc partie de la même famille de génératrices
que
et
elle est donc sécante avec
ce qui est absurde.
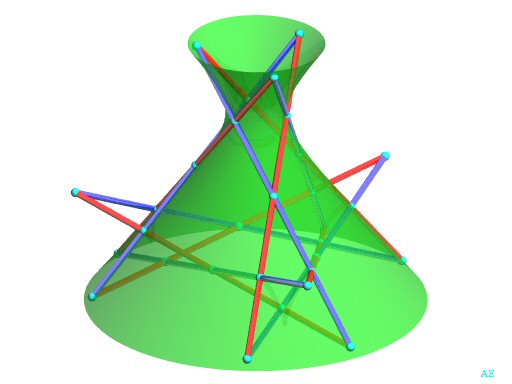 |
Vue de la quadrique (Q) contenant les 6 droites |
2) Preuve de la sécance de (tirée
de Geometry and the imagination, Hilb. et C.V., page 168)
Soit D une sécante commune à ,
et D' une sécante commune à
; les droites
rencontrent les 3 droites
et sont donc incluses dans la quadrique que ces 3 droites engendrent ;
or les droites
sont aussi incluses dans la surface cubique (S) contenant le double
six ; elles ne peuvent être distinctes, car sinon, la surface (S)
serait décomposée en une quadrique et un plan ce qui
est absurde ; donc D = D' est une sécante commune à
; elle n'est donc autre que
qui est donc sécante à
.