Famille de surfaces étudiée par Goursat en 1887. Edouard Goursat (1858 - 1936) : mathématicien français.

Les surfaces octaédriques (mieux vaut éviter "cubiques") de Goursat sont les surfaces quartiques ayant les symétries du cube (ou, ce qui revient au même, de l'octaèdre).
Plus précisément, ce sont les quartiques dont le groupes des isométries les laissant invariantes est le même que celui du cube.
La forme générale de leur équation en coordonnées cartésiennes est .
Voici quelques cas particuliers remarquables :
 

Vue obtenue par Maple	(k, k', k")	Équation, commentaires	Vue povray, par Alain Esculier
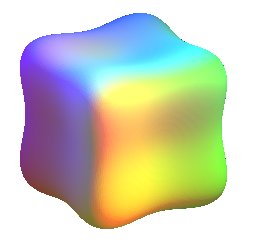	(0, –1, 0)	Cube arrondi passant par les sommets, les milieux des arêtes , et les centres des faces  du cube : .
	(–1,–1/4,1/4)	Octaèdre arrondi passant par les sommets  et les milieux des arêtes  de l'octaèdre: .
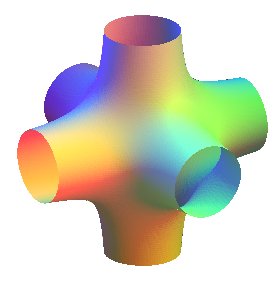	(–1, 1, 1)
	(0, –2, 2)	Surface possédant 12 points singuliers  aux sommets d'un cuboctaèdre.
	(–1/2, -1, 1/2)	Surface contenant les 12 arêtes prolongées de l'octaèdre: , par exemple . Elle est à l'octaèdre ce qu'est la surface de Cayley au tétraèdre.
	(–1/2, 1, -3/2)	Surface contenant les 12 diagonales des faces du cube , par exemple x = y , z= a. Elle est au cube ce qu'est la précédente à l'octaèdre.
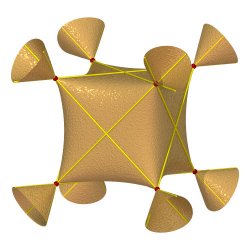	(–1, 4, –6)	. Surface contenant les 12 arêtes prolongées du cube , par exemple x = y = a.
		Même surface que précédemment !
	(–1, 2, –2)	Surface possédant 12 points singuliers  aux sommets d'un cuboctaèdre et contenant les 12 médianes prolongées des faces d'un cube, par exemple, z = 0, x = a. Elle est formée de 6 nappes de bases les faces carrées du cuboctaèdre.
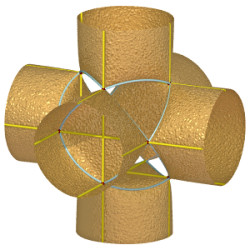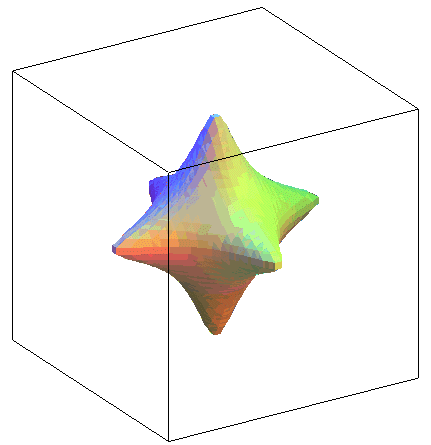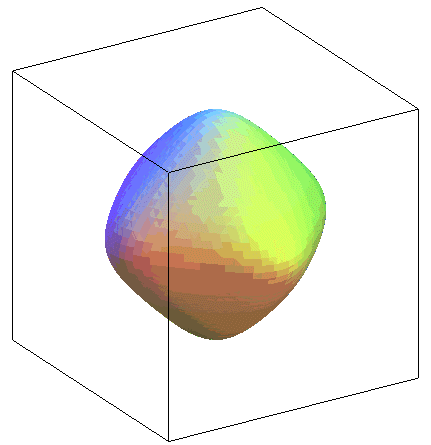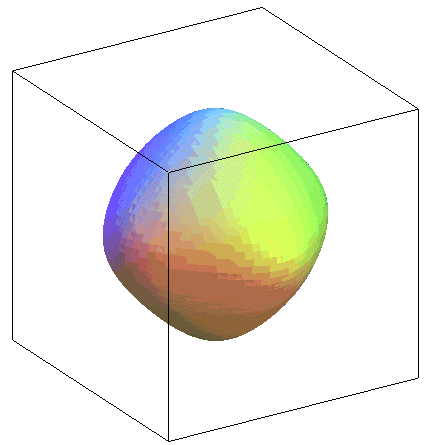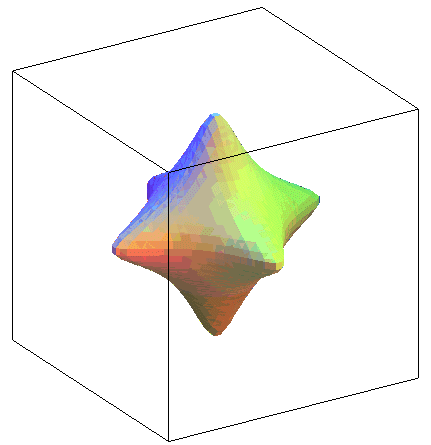
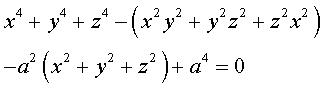
	(-1/3,-2/3,2/3)	Surface possédant 12 points singuliers  aux sommets d'un cuboctaèdre. Elle est formée de 8 nappes de bases les faces triangulaires du cuboctaèdre.

 

Animation du cas  plus un exemple avec k" = 0,02.

Plus généralement, les surfaces de Goursat sont les surfaces algébriques ayant les symétries d'un polyèdre régulier, les plus simples après la sphère (c'est-à-dire de degré minimal supérieur ou égal à 3).

Les surfaces tétraédriques de Goursat sont de degré 3, et ont pour équation générale .
Pour k' = 0, on obtient la surface de Titeica;, et dans les autres cas, quitte à changer a en a/k', on peut supposer k' = 1, et on obtient la famille à un paramètre  qui se comporte comme suit :
 

k < 0, k = 0 Quatre nappes, plus, dans le cas k = 0, le point O isolé.	0 < k < 4 Un tétraèdre arrondi plus 4 nappes.	k = 4 Surface de Cayley	k > 4

Vues de la quartique d'équation  qui possède les symétries du tétraèdre (remarquer les 4 points "triconiques ",  avec un nombre impair de signes moins).

Les surfaces dodécaédriques de Goursat sont de degré 6, et ont pour équation générale :

Quelques cas particuliers remarquables :
 

	(k, k',k",k''')	Équation, commentaires
	(0, 0, 0, 0)	soit Surface se décomposant en les 6 plans passant par les arêtes d'un icosidodécaèdre(le plan z = 0, le plan z = 2x et ses 4 images par les rotations d'angle  autour de Oz).
	(1,–1,1,–1)	Dodécaèdre arrondi.
	(–1,0,–1,1)	Icosaèdre arrondi
	(0,1,–2,1)	Surface possédant 30 points singuliers aux sommets d'un icosidodécaèdre. Elle est formée de 20 nappes de bases les faces triangulaires de l'icosidodécaèdre.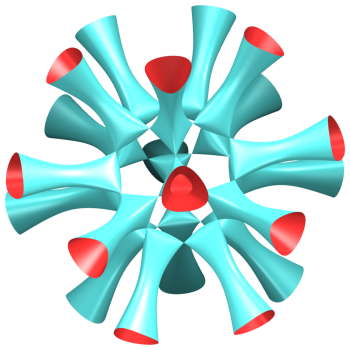
	(0,–1,2,–1)	Surface possédant 30 points singuliers aux sommets d'un icosidodécaèdre. Elle est formée de 12 nappes de bases les faces pentagonales de l'icosidodécaèdre.
	(0,5/4,–5/2,5/4)	Sextique de Barth, possédant 50 points singuliers.

 

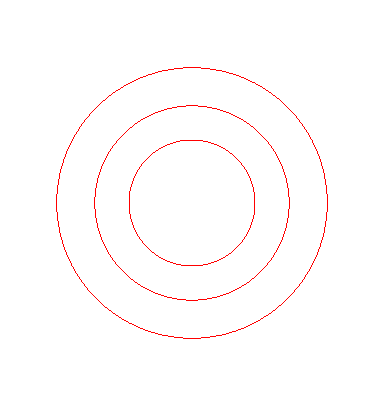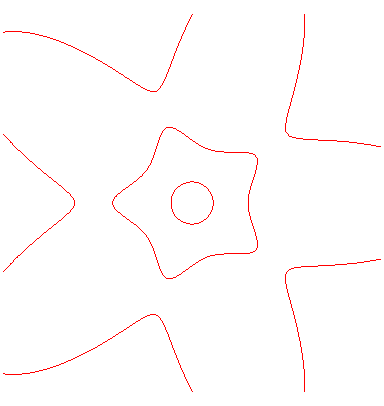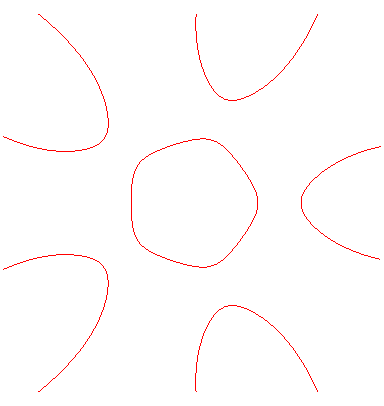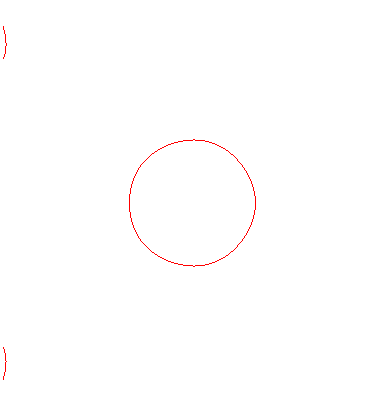
On peut imposer à la surface d'équation donnée ci-dessus de contenir une droite ne passant pas par O, et on constate que lorsqu'il existe une solution, la surface possède alors exactement 60 droites, images de l'une d'entre-elles par les 60 rotations du groupe des isométries du dodécaèdre. Par exemple, la valeur de (k, k',k",k''') pour que la surface contienne la droite x = 0, y = a  est (–1, 8, –18, 11) ; dans ce cas, les droites se regroupent en 6 groupes de 10 droites parallèles formant six "cylindres" dont les axes sont ceux qui joignent les sommets opposés d'un icosaèdre régulier. Voir ci-contre une animation montrant la section de la surface par une boule centrée en O, et à droite, une animation des sections horizontales. Un autre cas où on obtient (k, k',k",k''') formé d'entiers est (0, 5, –45, 71) ; la surface contient alors la droite  x=z=a, et 59 autres (ref : article de Goursat ci-dessus, page 198).

Voir d'autres superbes sextiques de Goursat en relief sur cette page d'Alain Esculier.

Voir aussi les courbes de Goursat, les surfaces retournables, les surfaces à symétrie de rotation.

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2018