An algebraic 3-dimensional curve is the intersection of two algebraic surfaces. Its degree is the product of the degrees of the two surfaces; it is also the number (with multiplicity) of (complex and projective) intersection points between the curve and any given plane.

A curve which is the intersection of two algebraic surfaces can be decomposed into the reunion of curves with smaller degrees the sum of which is equal to the degree of the whole curve.

The  algebraic 3D curves of degrees 1 and 2 are the lines and the conics.

The 3D cubics, of degree 3, are the intersections between two ruled quadrics that share a common line.
Examples: the skew parabola, the horopter.

The 3D quartics, of degree 4, can be divided into two groups:
 - first kind: intersection between quadrics that do not share a common line (called biquadratics : 4 = 2 . 2)
 - second kind: intersection between a cubic surface and a ruled quadric that have two common lines ().
Example: the striction line of a one-sheeted hyperboloid.

The names are the same as for plane curves (which are special cases).
Example of biquartic: the Archytas curve.

Examples of families of  algebraic 3D curves with any degree:
    - the 3D Lissajous curves (including the cylindrical sine waves)
    - the clelias.

Example of section between two algebraic surfaces, showing that the right framework for all this is complex projective geometry:
Intersection between Plücker's conoid (degree 3): 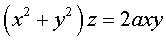 and the degree 2 cylinder: 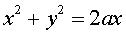; in homogeneous coordinates 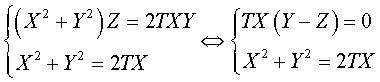. Therefore, the intersection is composed of the ellipse  (degree 2), the double line 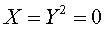 and the two imaginary lines 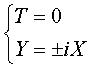: one can verify that 6 = 2 + 2 + 1 + 1.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2018