ARCHYTAS CURVE
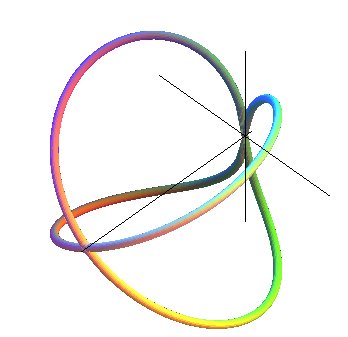
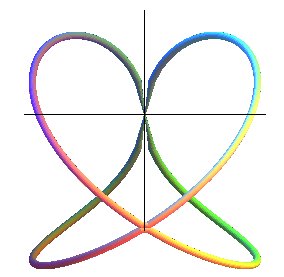
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ARCHYTAS CURVE

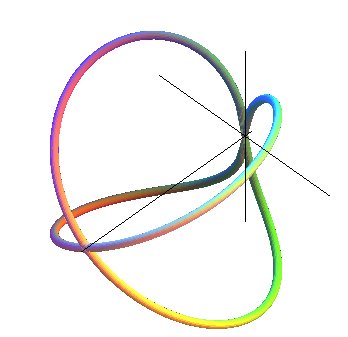
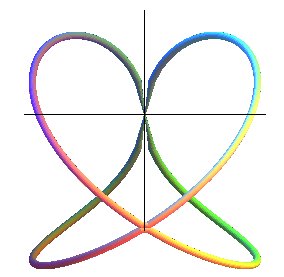
| Archytas
of Tarentum (430-350 B.C.) : Greek general, scholar and statesman.
This curve is supposed to be the first non planar curve studied in history. |
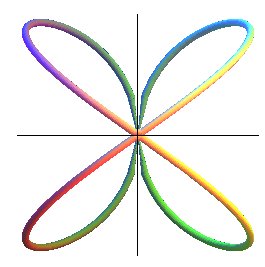
| System of Cartesian equations: Système cylindrical equations : Système spherical equations : Algebraic curve of degree 8 (3D biquartic). Cartesian parametrization: |
| The Archytas curve is the intersection between a horn torus and a cylinder of revolution with axis perpendicular to the central circle of the torus and with the same radius. |
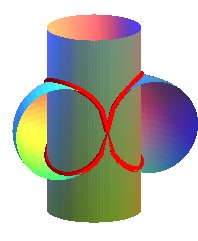 |
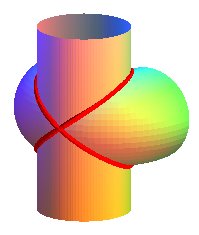 |
|
Construction of the curve: The torus is produced by a circle (CQ) of horizontal diameter [OQ], the point Q having a movement circular around O, and the cylinder, by a vertical line (D) passing through P, the point P describing a fixed circle of diameter [OA] (OQ = OA). Taking P on (OQ), the point M of intersection of (D) with (CQ) describes the Archytas curve. Analytically: |
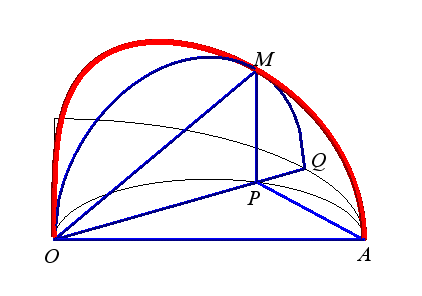 |
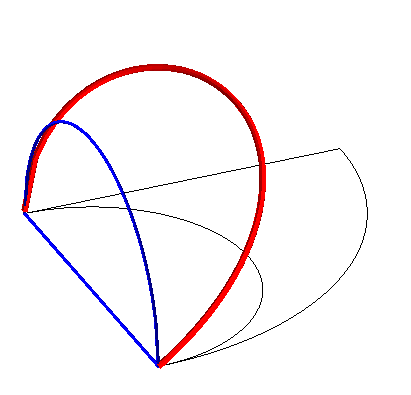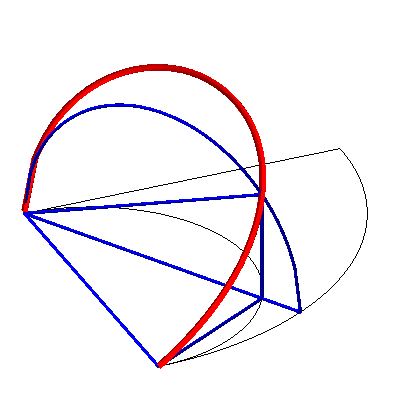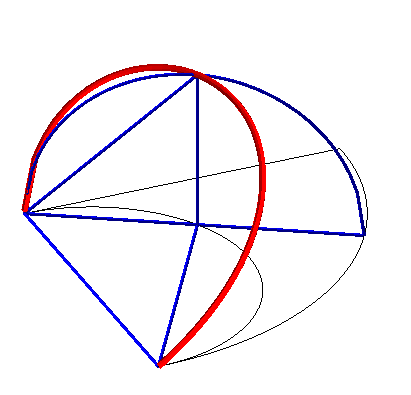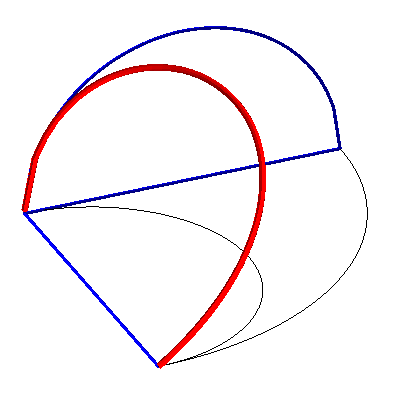 |
It was studied by Archytas because it is a duplicatrix:
indeed,
therefore, if
,
then
;
In this configuration, the two numbers
and
appear simultaneously as ratios of lengths, but to obtain
this configuration, it is necessary to know
which is not constructible.
| This can be generalized to any torus and we can consider
the intersection between the torus As a is larger, the curve tends to a bicylindrical curve (case of the double ellipse). |
 |
Compare to bitorics.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2023