ISOPTIC CURVE
The isoptic with angle 
of the cardioid is composed of two limaçons of Pascal.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ISOPTIC CURVE
The isoptic with angle
of the cardioid is composed of two limaçons of Pascal.
| Curve studied by La Hire in 1704 and Chasles in 1837.
From the Greek Isos "equal" and optikos "relative to sight". Name given by Taylor in 1884. |
In differential geometry, the isoptic (curve)
with angle 
of a curve is the locus of the points through which pass two tangents to
the curve forming an angle 
.
| A method to obtain the equation of the isoptic of the curve f (x, y) = 0: eliminate x1, y1, x2, y2 between the 5 equations: f (x1, y1) = 0, f (x2, y2) ) = 0, p (x1, y1) * (x-x1) + q (x1, y1) * (y-y1) = 0, p (x2, y2) * (x-x2) + q (x2, y2) ) * (y-y2) = 0, and tan (alpha) = (p (x1, y1) -p (x2, y2)) / (1 + p (x1, y1) * q (x2, y2)). |
Examples:
- the isoptics of the parabola  are
hyperbolas (with same focus and directrix as the parabola), with equation:  .
On the right, the case of an angle 
(the other branch of the hyperbola would give the supplementary angle). |
 |
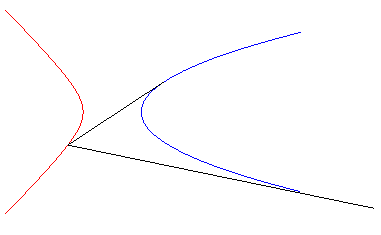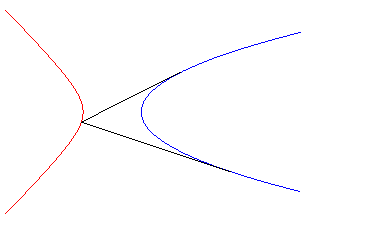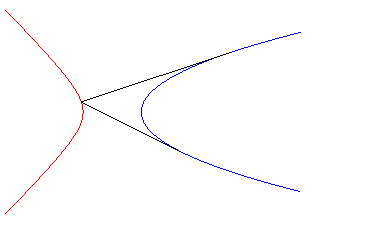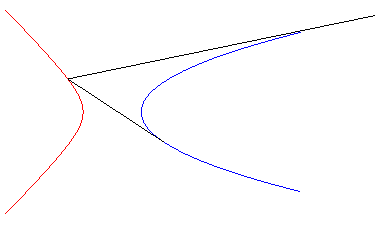- the isoptics of the centred conics
are the plane spiric curves: for the
conic 
,
the isoptic curve has equation 
(Loria
2D tome 2 p. 156).
- the isoptics of the (- epi,
- hypo) trochoids are
the reunions of (- epi, - hypo) trochoids (see the example of the cardioid
above).
- the isoptics of sinusoidal
spirals are sinusoidal spirals.
A related notion in metrical geometry, bearing the same
name, is that of isoptic with angle
of a part X of the plane: locus of the vertices of the angular domains
of angle
that circumscribe X (i.e. that contain X, and the two sides
of which intersect with X).
Examples:
- the isoptics of a segment line are
the circles a chord of which is this segment line (theorem of the capable
arc).
A different notion was also referred to as isoptic: the isoptic of two parts X and Y of the plane is the locus of the points of the plane where X and Y are "seen" under the same angle, more precisely, the locus of the vertices of two angular sectors of same angle, one of which circumscribes X while the other circumscribes Y.
When the two parts X and Y are segment lines, we get the isoptic cubics.
The case of two circles with centres 
,
and radii 
is much simpler: we get the circles of
Apollonius with equation 
.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017