next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

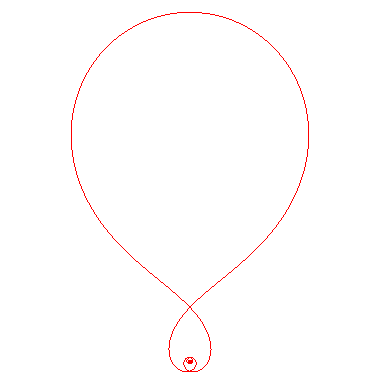
INVERSE NORWICH SPIRAL

Curve studied by Masurel in 2013.
Homemade name.

 
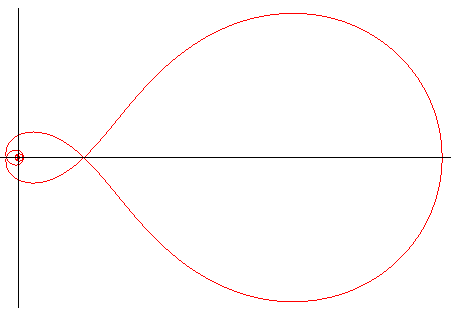
Polar parametrization: .

Curvilinear abscissa: s = a t.

Cartesian tangential angle: .

Radius of curvature: .
Intrinsic equation 1: .
Length: .

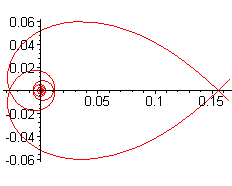The inverse Norwich spiral is, as indicated by its name, the inverse of the Norwich spiral with respect to the pole.
 
 
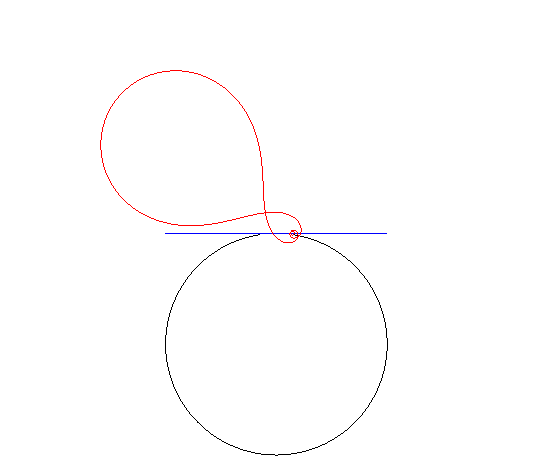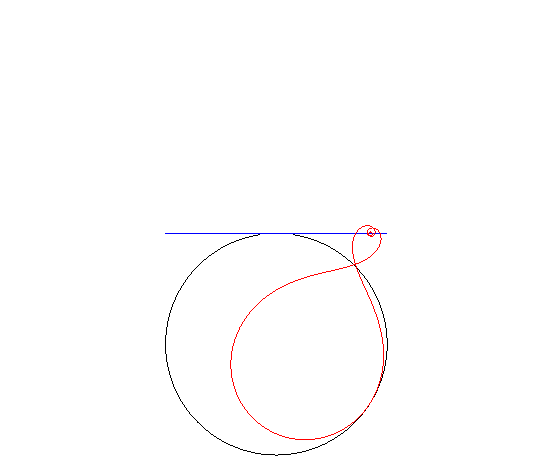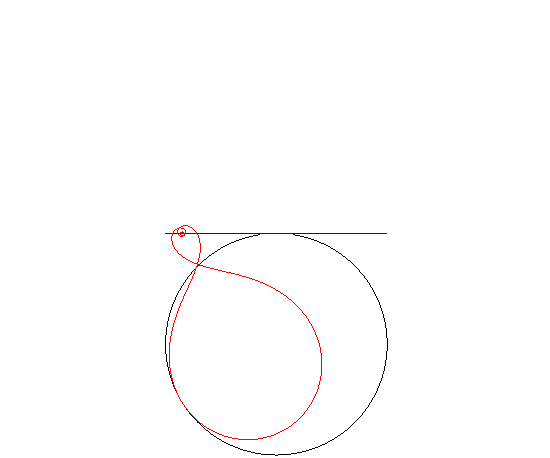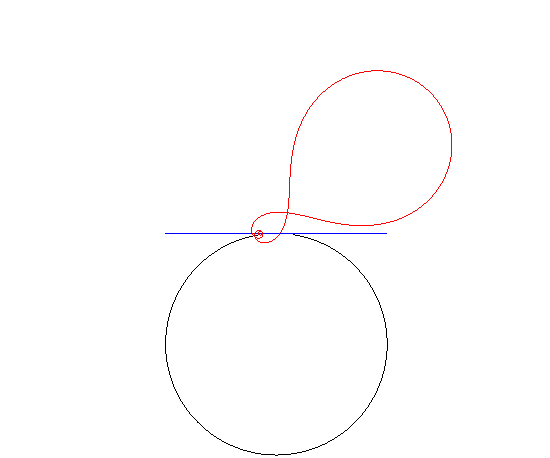
This curve has the particularity of being the "wheel" which, when rolling on a circular "road", is such that the hub describes a tangent to the circle. 

See this page.

However, if the inverse Norwich spiral rolls on a line, then the pole describes a cardioid.

 
 
 
next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

© Robert FERRÉOL  2017