Courbe de Holditch

HOLDITCH CURVE

Curve studied by Holditch in 1858, H. Benitez in 1980, et Monterde & Rochera in 2017.
Animations below made by Alain Esculier.

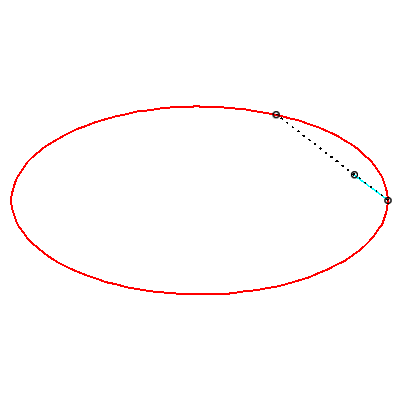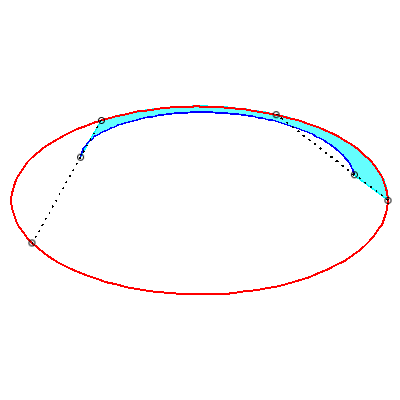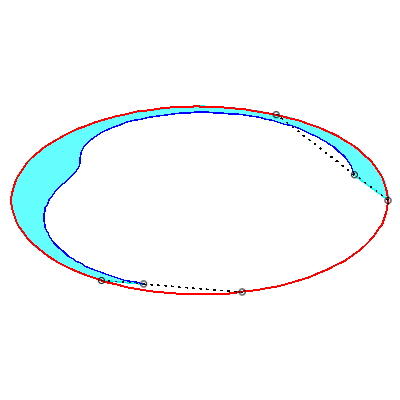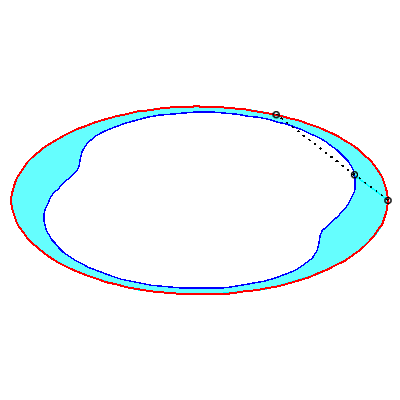
To obtain the Holditch curve of , of equation f(x, y) = 0 : eliminate between the equations, with .

The Holditch curves associated with a given curve are the locations of the fixed points M of a straight line whose two fixed points A, B, belong to . Holditch considered these curves because when is closed, and under certain conditions, he prooved that the difference between the area enclosed by and that enclosed by the Holditch curve is , where (see the Holditch theorem).
These curves are cases of glissettes, the two points A and B "sliding" on the curve (see the special case number 2 in the page on the glissettes).

Obtaining the equation of the Holditch curve is usually difficult, but here are two simple cases:

For an ellipse:, with a chord of length 2c, the plotter point being at the center, the Holditch curve has a Cartesian equation: (quartic of genius 2).
Polar equation : .
For an hyperbola, change the sign in front of y².
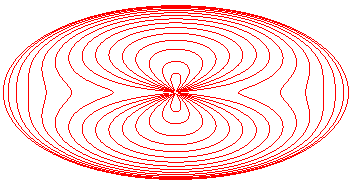
Loss of convexity for c > p = b²/a.

For a parabola:, the Holditch curve, for a chord of length 2c, the tracer point being located in the center, has a Cartesian equation: (quartic).
Loss of convexity for c > p .

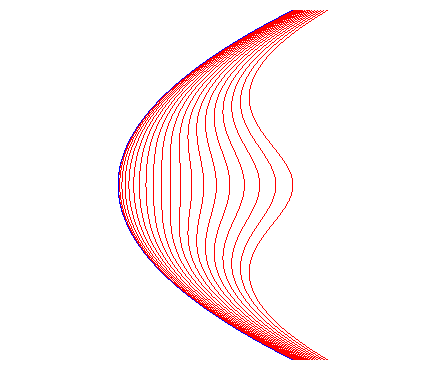Here is the evolution of the complete Holdich curve of the ellipse, for a plotter point located between A and B, out of the center, rope length 2c. For , it is formed of two continuous curves symmetrical with respect to the axis of the ellipse.
Each curve is ...

convex for ,

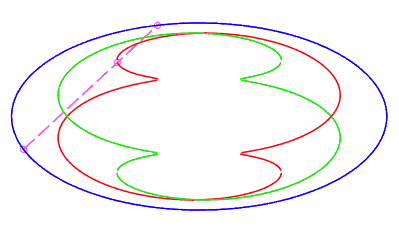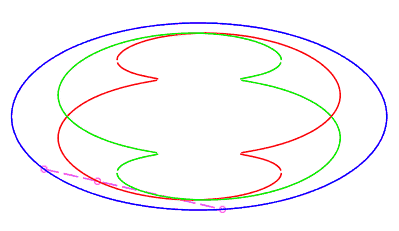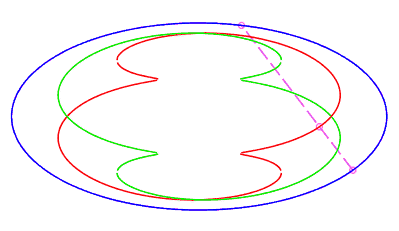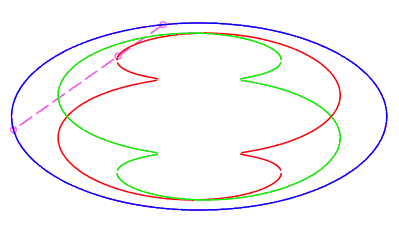
closed without a double point, traversed in a movement without retrograde phase, where the rope returns to its starting point after having made a complete turn, for ,

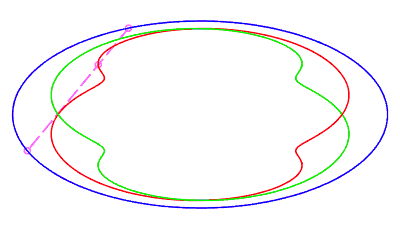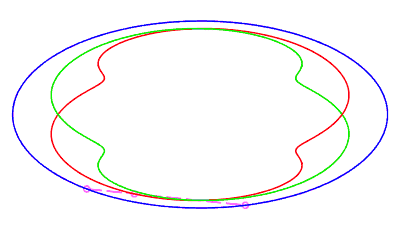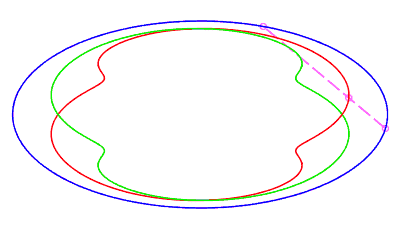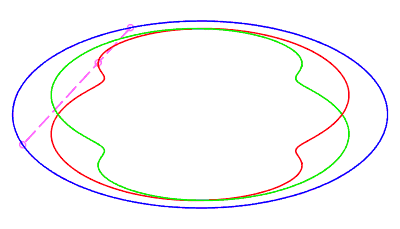closed without a double point, traversed by a movement with retrograde phase, where the rope returns to its starting point after having made a complete turn, for .
The number d is the minimum half-length of a chord whose end is perpendicular to the ellipse (instant ending the retrograde phase, see the animation opposite).

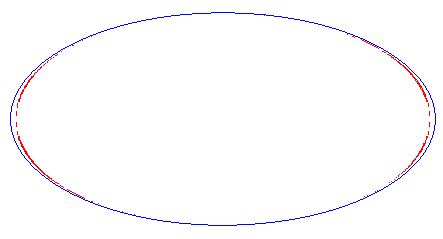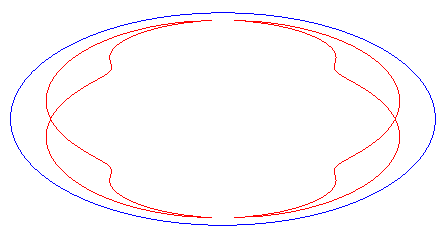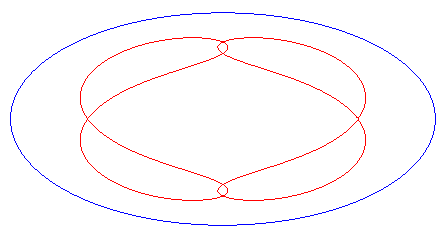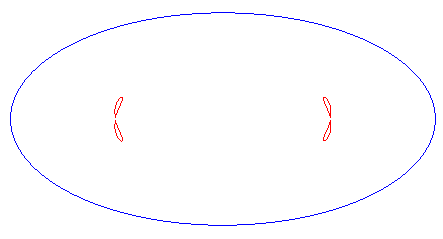
eight shaped, traversed by a movement with a retrograde phase where the rope returns to its point of departure without rotation, for b < c < a.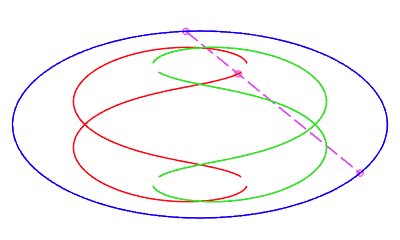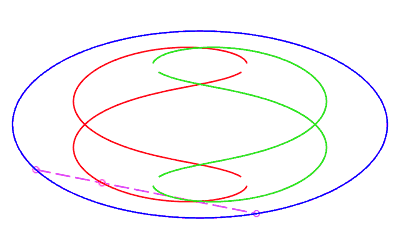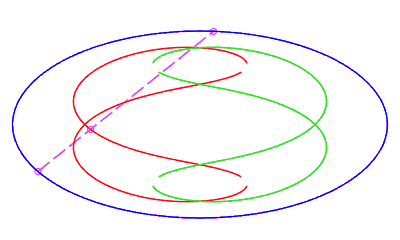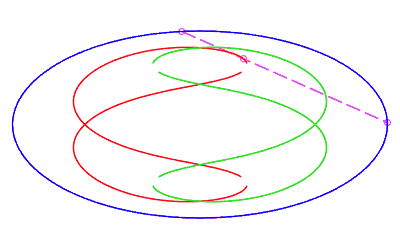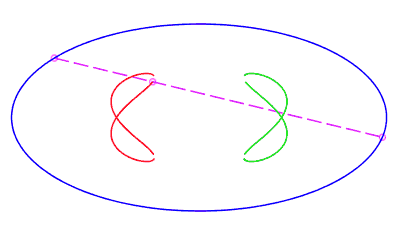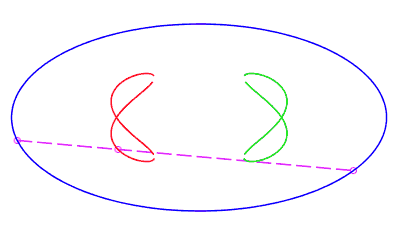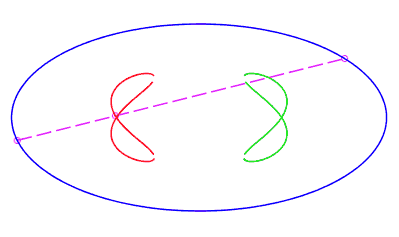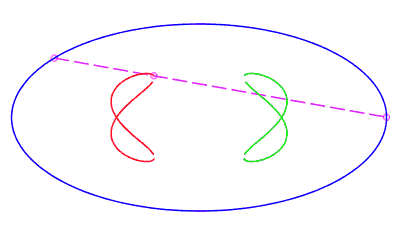

Animation of the deformation of the complete curve for 0 < c < a.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

For an ellipse:, with a chord of length 2c, the plotter point being at the center, the Holditch curve has a Cartesian equation: (quartic of genius 2). Polar equation : . For an hyperbola, change the sign in front of y².	Loss of convexity for c > p = b²/a.
For a parabola:, the Holditch curve, for a chord of length 2c, the tracer point being located in the center, has a Cartesian equation: (quartic). Loss of convexity for c > p .

convex for ,
closed without a double point, traversed in a movement without retrograde phase, where the rope returns to its starting point after having made a complete turn, for ,
closed without a double point, traversed by a movement with retrograde phase, where the rope returns to its starting point after having made a complete turn, for . The number d is the minimum half-length of a chord whose end is perpendicular to the ellipse (instant ending the retrograde phase, see the animation opposite).
eight shaped, traversed by a movement with a retrograde phase where the rope returns to its point of departure without rotation, for b < c < a.
Animation of the deformation of the complete curve for 0 < c < a.