| bibliographie | introduction | courbes 2D | Retour accueil | surfaces | fractals | polyèdres |
|
|
|
|
|
|
|
|
|
|
ARÊTE DE REBROUSSEMENT D'UNE SURFACE RÉGLÉE DÉVELOPPABLE
ASYMPTOTIQUE D'UNE SURFACE (LIGNE/)
BILLARD CYLINDRIQUE (NOEUD DE/)
BILLARD RECTANGULAIRE (NOEUD DE/)
BRUNNIEN (ENTRELACS/)
CAPAREDA (COURBES DE/)
COURBURE CONSTANTE (COURBE À /)
CYLINDRO-CONIQUE
(COURBE/)
DÉCLIVITÉ
EXTRÉMALE (LIGNE DE/)
ÉCHELLE DE JACOB
ENVELOPPE D'UNE FAMILLE DE COURBES A UN PARAMETRE
GRAPHE ASSOCIÉ A UN ENTRELACS GRAPHE2
HÉLICE DE L'HYPERBOLOÏDE DE RÉVOLUTION
HÉLICE DU PARABOLOÏDE DE RÉVOLUTION
HYPOCYCLOÏDE SPHÉRIQUE
INDICATRICE SPHÉRIQUE
DE COURBURE (D'UNE COURBE 3D)
INDICATRICE SPHÉRIQUE DE TORSION (D'UNE COURBE 3D)
LIGNE TRACÉE SUR UNE SURFACE
LIGNE
DE COURBURE,
ASYMPTOTIQUE,
GÉODÉSIQUE,
PSEUDO-GÉODÉSIQUE
LIGNE TOPOGRAPHIQUE :
DE NIVEAU,
DE
PENTE, DE TALWEG, DE
CRÊTE
NOEUD DE BILLARD RECTANGULAIRE
PELURE D'ORANGE (COURBE DE LA/)
PENTE (LIGNE DE/, ou LIGNE DE PLUS GRANDE/)
PIRONDINI (SPIRALE CONIQUE DE/
PRÉCESSION CONSTANTE (COURBE DE/)
RELÈVEMENT D'UNE COURBE PLANE SUR UNE SURFACE
SEIFFERT (SPIRALE SPHÉRIQUE DE/)
STRICTION D’UNE SURFACE RÉGLÉE NON DÉVELOPPABLE (LIGNE DE/)
TORSION CONSTANTE (COURBE À /)
TRACTOIRE
: courbe en cours d’étude.
M : point courant de la courbe.
repère orthonormé direct, d’axes Ox , Oy et
Oz.
: coordonnées cartésiennes de M.
:
coordonnées cylindriques (ou semi-polaires) de M ;
![]() .
.
ou
: coordonnées
sphériques de M (
est la longitude,
est la latitude et
la colatitude).
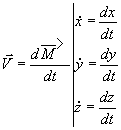 ,
vecteur vitesse, V : vitesse algébrique.
,
vecteur vitesse, V : vitesse algébrique.
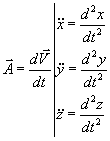 ,
vecteur accélération.
,
vecteur accélération.
(T) : tangente, dirigée par .
(P) : plan osculateur, dirigé par
et
.
(N) : normale principale, orthogonale à (T), dans le plan osculateur.
(B) : binormale, orthogonale à (P),
dirigée par .
s : abscisse curviligne
(![]() ,
, ![]() )
)
(voir aussi cette page pour l'abscisse curviligne d'une courbe tracée sur une surface)
![]() : vecteur tangent (unitaire).
: vecteur tangent (unitaire).
V : vitesse absolue ().
: vecteur normal (unitaire), dirigeant la normale principale ; le plan
(M,
![]() ,
,![]() )
est le plan osculateur en M.
)
est le plan osculateur en M.
![]() : centre de courbure en M.
: centre de courbure en M.
![]() : vecteur binormal =
: vecteur binormal =
(unitaire) (
= base, ou trièdre de Frénet).
: rayon de courbure, toujours positif ou nul.
![]() est l'angle entre
est l'angle entre ![]() et
et ![]() , donc
entre deux tangentes infiniment voisines ;
, donc
entre deux tangentes infiniment voisines ;
est l'angle de courbure ; il représente la longueur du chemin
parcouru par l'extrémité du vecteur tangent attaché
à un point fixe.
: rayon de torsion pour une courbe gauche.
,
défini par
![]() est l'angle entre deux plans osculateurs infiniment voisins ; la convention
de signe que nous avons prise, dite convention de Darboux, est telle que
les courbes dextres ont une torsion positive
; son signe est indépendant du sens de parcours ;
est l'angle entre deux plans osculateurs infiniment voisins ; la convention
de signe que nous avons prise, dite convention de Darboux, est telle que
les courbes dextres ont une torsion positive
; son signe est indépendant du sens de parcours ;
est l'angle de torsion ; il représente la longueur du chemin
parcouru par l'extrémité du vecteur binormal attaché
à un point fixe.
On a les formules de Frénet :![]() ,
, ![]() ,
,![]() .
.
:
courbure ; (
mesure l'intensité de la variation de la tangente) .
: torsion (
mesure l'intensité de la variation du plan osculateur).
D'où l'écriture condensée des formules
de Frénet : .
Centre du cercle osculateur : ,
centre de la sphère osculatrice :
.
Système d’équations, paramétrisation cartésienne : caractérisation en x, y et z.
Système d’équations, paramétrisation
cylindrique : caractérisation en ,
et
z.
Système d’équations, paramétrisation
sphérique : caractérisation en r, et
.
Voir les notations sur les courbes tracées sur
une surface à la page
sur les surfaces.
| bibliographie | introduction | courbes 2D | Retour accueil | surfaces | fractals | polyèdres |