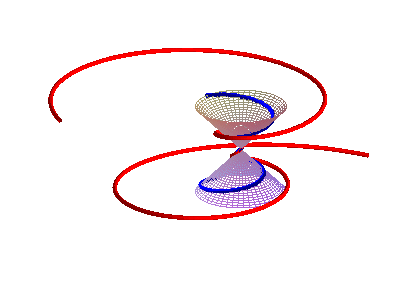
Involute of a conical spiral
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
INVOLUTE OF A CURVE, OF A DEVELOPABLE SURFACE
| Notion studied by Monge in 1771. |

Involute of a conical spiral
| If M0 is the current
point on Cartesian parametrization: Radius of curvature: |
I) Involutes of a curve.
The involutes of a curve
are the trajectories described by the points of a line rolling without
slipping on this curve.
Therefore, they trace, on the tangent
developable
of
, the
orthogonal trajectories to these tangents; they also form an equivalence
class of parallel curves.
They are also the curves for which the initial curve
is an evolute.
When the surface
is developed on a plane, the 3D involutes become the 2D involutes
of the image of
on this plane.
An involute is planar iff the initial curve is a helix.
In this case, all the involutes are planar.
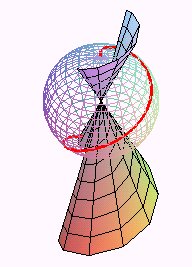
II) Involutes of a developable surface.
The involutes of a developable
surface
are the trajectories of a point on a plane rolling without slipping on
the surface
;
therefore, they are the curves for which the initial surface is the polar
developable. They present a cuspidal point on
,
with a tangent that is orthogonal to
;
and they form an equivalence class of parallel
curves.
When
is a cylinder, the involutes are the involutes of the planar sections perpendicular
to the axis.
When
is a cone, the involutes are traced on spheres centered on the vertex of
the cone: they are the loci of a point on a circle centered on the vertex
of the cone rolling without slipping on an orthogonal trajectory of the
generatrices of the cone.
| In the case of a cone of revolution, they are spherical helices. |
 |
Problem: how to derive the parametrization of the involutes of from
the parametrization of its cuspidal edge ????
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018