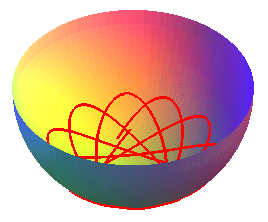
CURVE OF THE SPHERICAL PENDULUM

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CURVE OF THE SPHERICAL PENDULUM



| Curve studied by Clairaut in 1735, Lagrange (mécanique
analytique), and Puiseux
in 1842.
Other name: curve of the conical pendulum. See: Paul Appell : cours de mecanique rationnelle, page 530. Wikipedia article |
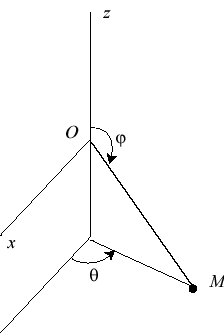
| Differential equation of the motion (derived from
Newton's second law):
where q = longitude, j = colatitude and First integral: Spherical differential equation of the curve: i.e., with 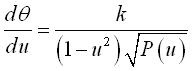
where note the tiny difference with the spherical catenary, for which |
 |
The curve of the spherical pendulum is the curve described
by the end of a simple massive pendulum attached to a fixed point, that
can move in three dimensions, and placed in a uniform gravitational field
(here ).
This curve is traced on a sphere, and is none other than a flow line of this sphere: it can be physically obtained by making a ball roll inside a sphere.
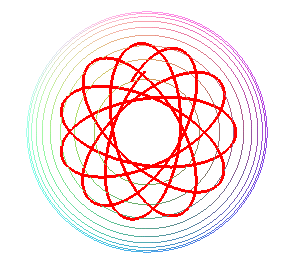
Like the case of the spherical catenaries, we get curves composed of a sequence of undulations joining alternatively two parallels (obtained for the values at which the polynomial P above cancels), and images of one another by rotations around Oz. The curve is either closed, or dense in the zone between the two parallels.
 |
 |
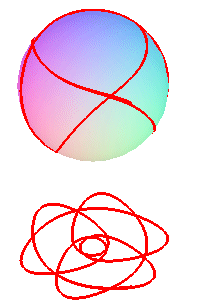 |
 These acrobat
bikers of the Shanghai circus describe such curves.
These acrobat
bikers of the Shanghai circus describe such curves.
These curves can be generalized by considering the Coriolis
force, which give the following differential equation of the motion: .
When the pendulum is dropped without an initial speed,
we get the curve of the Foucault pendulum, which, for small oscillations,
can be approached by a hypocycloid.
Without the Coriolis force, the curve would amount to
an arc of a circle.
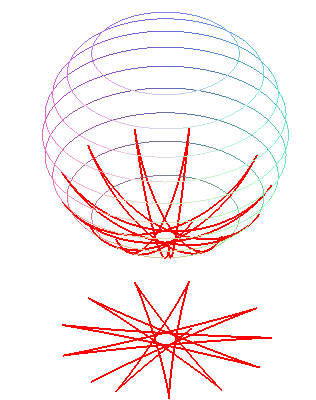 |
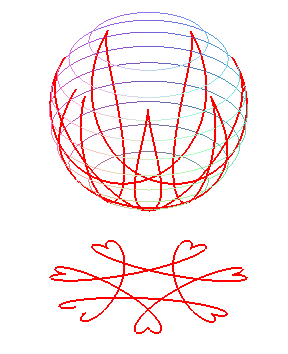 |
 |
Here is a view of the curve described by a pendulum in forced uniform rotation around Oz.
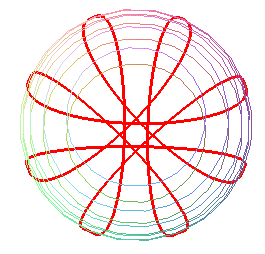 |
 |
See the spinning top
festoons, which are another generalization of the curves of the spherical
pendulum.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018