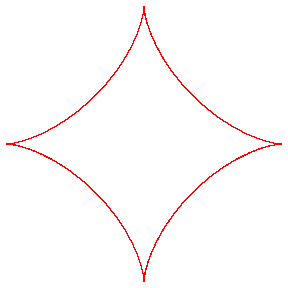
ASTROID
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ASTROID

| Curve studied by Rømer in 1674, Jean Bernoulli
in 1691, Leibniz in 1715 and D'Alembert in 1748.
Named by Littrow in 1838. "Astroid" comes from the Greek word "star" : "astron" (like the word "asteroid" designing star like objects). Other names : H4 (hypocycloid with 4 cusps), cubocycloid. |
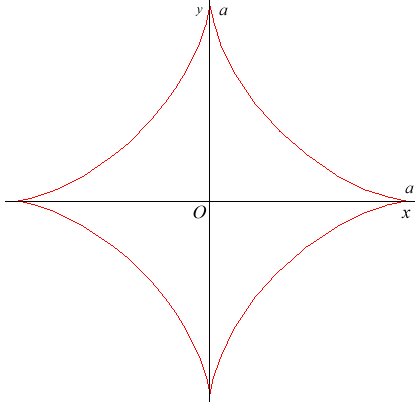 |
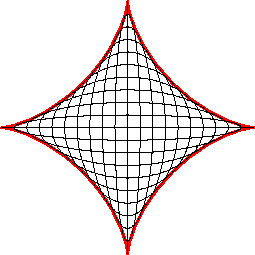
Parametric equation: Cartesian equation: Complex parametric equation: Cartesian tangential angle: 1) Curvilinear abscissa: 1) Radius of curvature: 1) Cesaro equation: Whewell equation: Pedal equation: Length of curve: 6a. Area enclosed: |
The astroid is a hypocycloid
with four cusps (a circle having a/4 (or 3a/4) for radius
running in a circle (C) having a for radius).
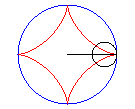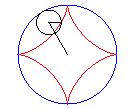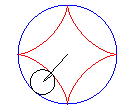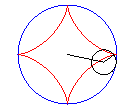 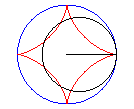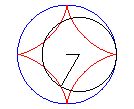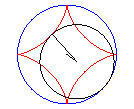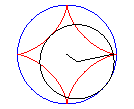 |
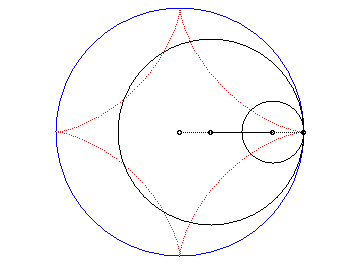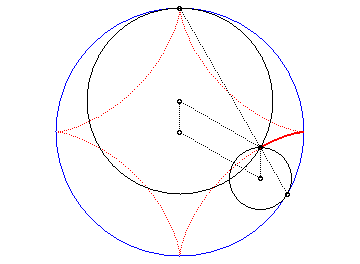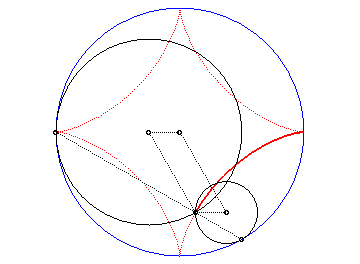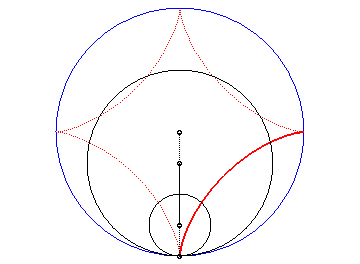
Animation of the double generation |
Then, it is the envelope of a chord (PQ) of the circle having the center O and a/2 for radius (inscribed circle of the astroid), P and Q running on this circle with opposite directions, one being three times faster than the other (Cremona generation).
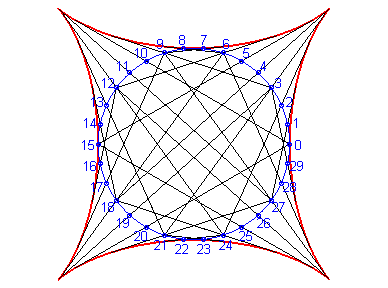
Above, the point n is linked to the point -3n modulo 30. |
 |
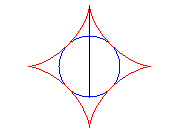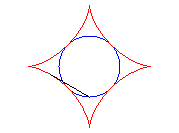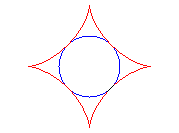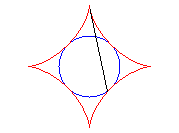 |
And it is also the envelope of the diameter of a circle having a/2 for radius running inside (C).
The ends of this diameter trace two perpendicular segments.
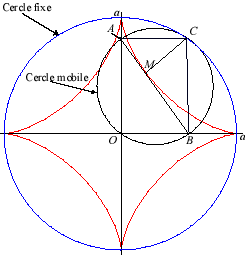
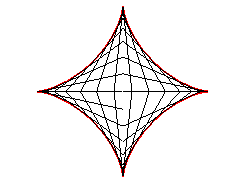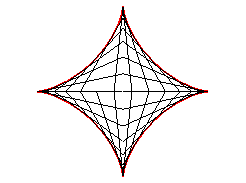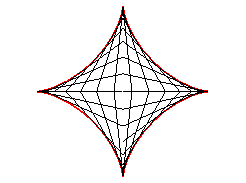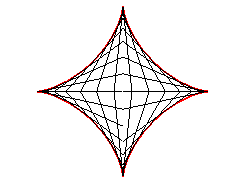
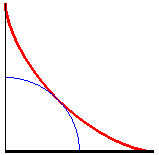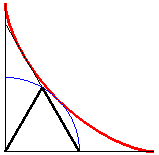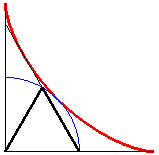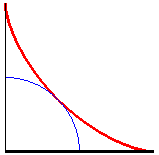
| Therefore, the astroid is also the envelope
of a segment [AB] with a length of a whose ends move along
two perpendicular lines. The contact point M is the projection of
the C vertex of the (OACB) rectangle on [AB] (and
the points of the line trace an ellipse).
The most general case where the lines are not perpendicular gives a tetracuspid. See also the Milk Carton which is the three dimensional generalisation of this envelope. |
 |
Based on this property, the edge of the mark of a two-panel sliding door of an autobus on the running board is an eighth of an astroid, followed by a circular arc.
Note: the curve determined by a string
art built on two perpendicular segments is not an astroid, but an other
Lamé
curve with 4 parabolic segments
(the [AB] segment does not have a fixed length).
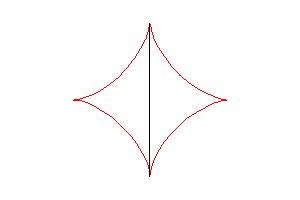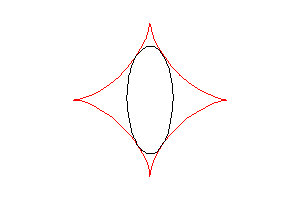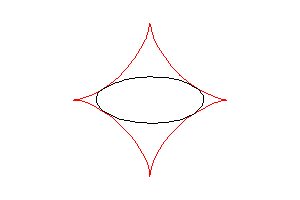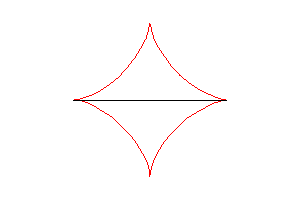
The astroid is also the envelope of the ellipses described
by , with
(two dimensionnal tracks of the ends of the [AB] segment above).
 |
 |
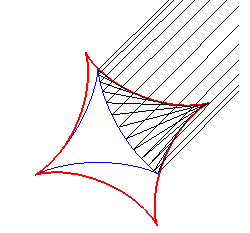
Finally, it is the evolute,
by reflection, of a deltoid, with parallel incident rays of any direction(needing
to understand how a symmetric curve of degree 3 can generate a symmetric
curve of degree 4).
 |
 |
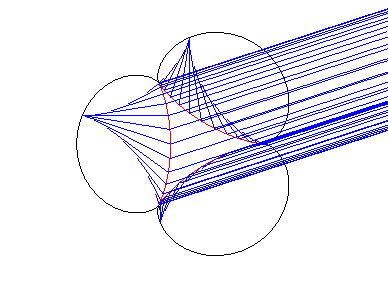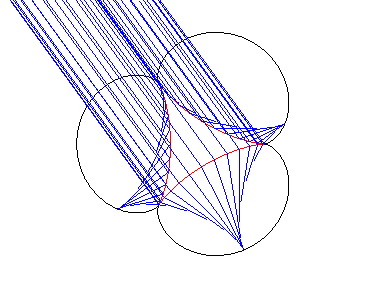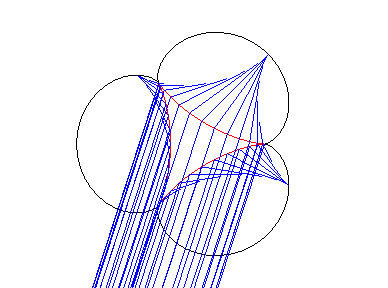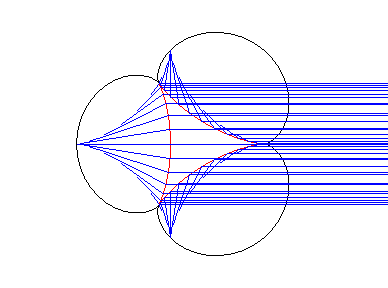
When incident rays follow every possible direction, the vertices of the astroid's envelope describe an epicycloid with 3 cusps. There is a similar property with theTschirnhausen's cubic. |
| As for any cycloid curve, the evolute of an astroid is a similar astroid (in a ratio of 2): | 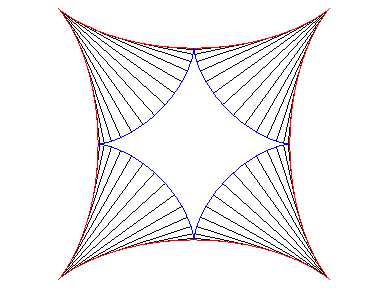 |
| One of the involutes is then an astroid; there are two others (see also Maltese cross): | 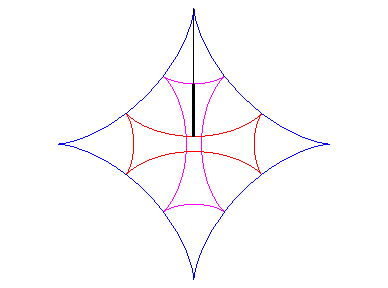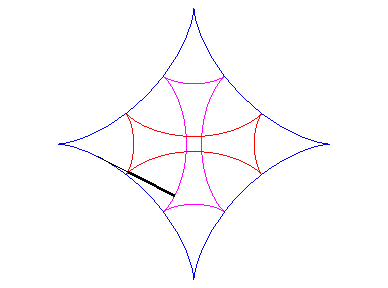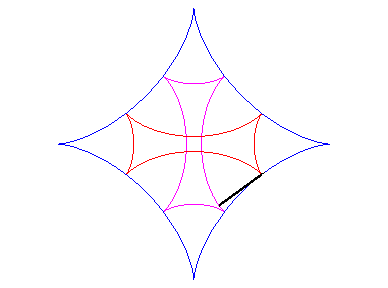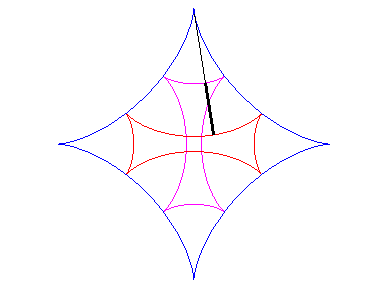 |
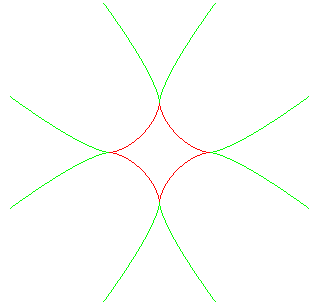
| The curve whose Cartesian equation is: It can be easily defined as the envelopes of the straight lines crossing Ox and Oy in P and Q while the sum or difference of OP² and OQ² stays constant. |
 |
Astroid pedals are beetle curves ; in particular, the pedal with respect to the centre is the quadrifolium, and the polar is the rectangular cross curve.
See also tetracuspid.

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2017