From the Greek Kampulos: curved Eudoxus of Cnidus (406 BC - 355 BC): Greek astronomer, mathematician and philosopher. Other name: Clairaut's curve.

 

Polar equation:  (Clairaut's curve). Cartesian equation:  or  (compare with that of Gerono's lemniscate). Rational quartic. Equation of the parabolic asymptotes: .

 

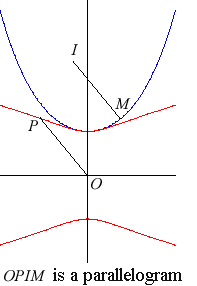
If for a point P travelling on a circle (C) of centre O, the tangent to C at P cuts Ox in Q, then the Kampyle of Eudoxus is the locus of the intersection point between the line (OP) and the line parallel to Oy passing through Q.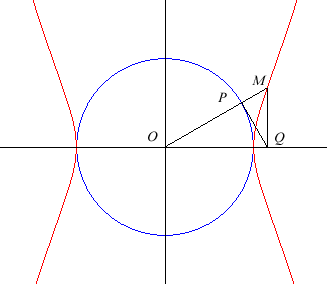

 

The Kampyle (in red, opposite) is also the locus of the focus of a parabola constrained to stay tangent to a straight line at a fixed point. Therefore, it is a glissette. For a parabola of parameter p, we get a Kampyle of parameter a = p/2.

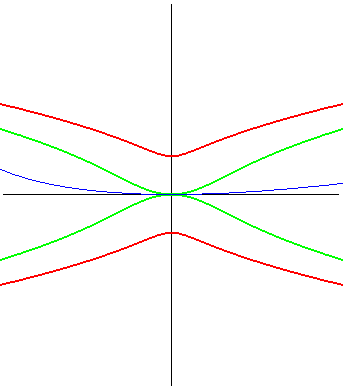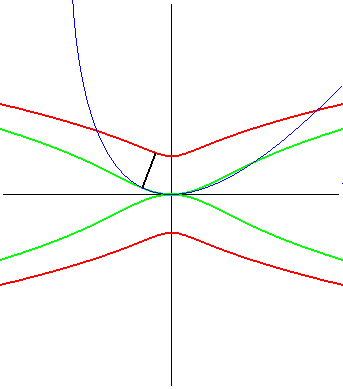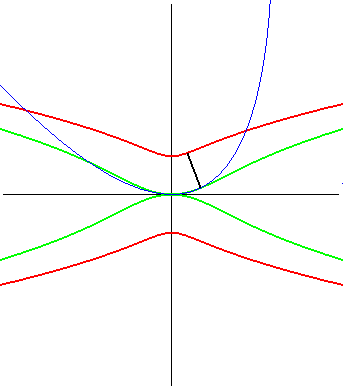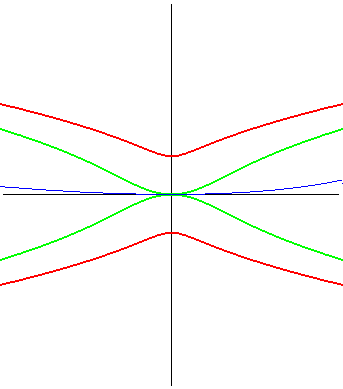The Kampyle of Eudoxus also is the radial curve of the catenary curve (here, up to rotation by an angle of p/2),

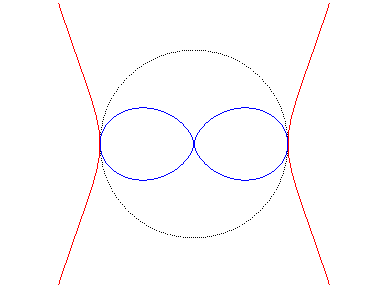
as well as the inverse of the double egg,

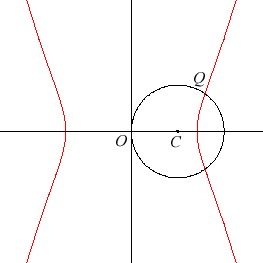
It was studied by Eudoxus because it is a duplicatrix. Indeed, its intersection point Q with a circle of centre C passing through O (equation  ) is at distance  of O.

The Kampyle can also be found as the rolling curve of the linear conchoidal motion, and as the base of the Kappa motion (see this page).
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017