Curves studied by Clairaut in 1726. Other name: Clairaut's multiplier curve.

 

Polar equation:  with n a real number (or ). Cartesian equation: . Algebraic curve if and only if n is rational.

Clairaut's curves are defined by their polar equation written above.

Examples for positive values of n (part with positive ordinate):

n = 1: circle	n  = 2: double egg	n = 3: simple folium
n = 1/2: curve of the dipole	n = 3/2	n = 5/2
n  = 1/3	n = 2/3	n = 4/3

Examples for negative values of n (part with positive ordinates):

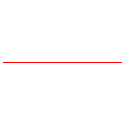
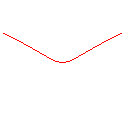
n = -1: line y = a	n  = -2: Kampyle of Eudoxus	n = -3: duplicatrix cubic
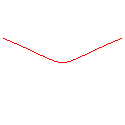
n =- 1/2:  cf. Külp's quartic	n = -3/2	n = -5/2
n  = -1/3 : cf witch of Agnesi	n = -2/3 : Roche's curve.	n = -4/3

 
 

Clairaut's curves are the glissettes of the sinusoidal spirals. More precisely, if the sinusoidal spiral of parameter n slides on a line at a fixed point, the glissette of the pole is Clairaut's curve of parameter 1/n: . Thanks to the glissette/roulette equivalence theorem (see at glissettes), Clairaut's curves are also the linear roulettes of the evolutes of the sinusoidal spirals. Examples:  for  n = 1/2: the double egg is the glissette of the cusp of the cardioid (cf animation) for n = 2:  the curve of the dipole is the glissette of the centre of the lemniscate of Bernoulli, pour n = -1/2: The Kampyle of Eudoxus is the glissette of the focus of the parabola, for n = - 1/3: the duplicatrix cubic is the glissette of the focus of the Tschirnhausen cubic.

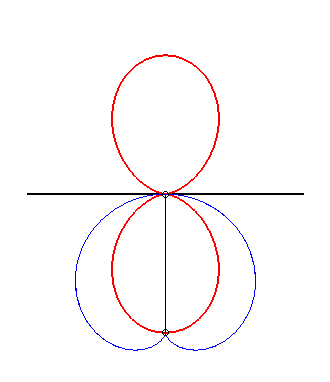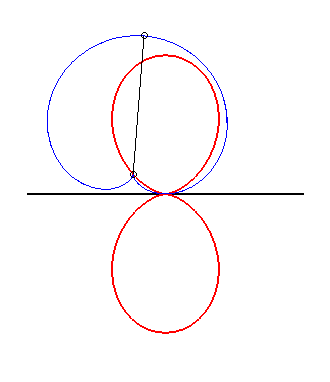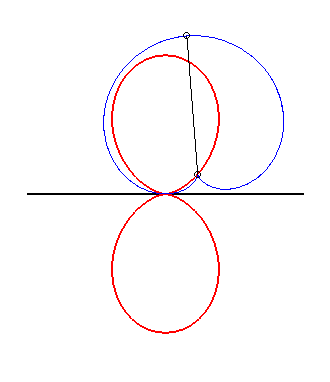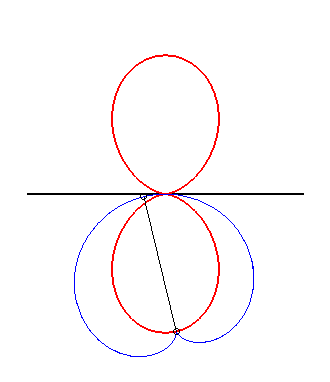The orthogonal trajectories of various Clairaut's curves of parameter n, , are the Clairaut's curves of parameter 1/n, . Opposite, the cases n = 1 and 2.

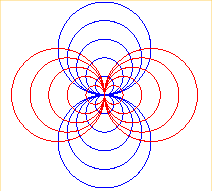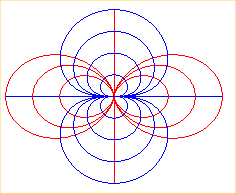Clairaut's curve of parameter n is also the radial curve of the Ribaucour curve of parameter n + 1.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017