CROIX DE MALTE
Maltese
cross, Maltakreuz
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CROIX DE MALTE
Maltese
cross, Maltakreuz

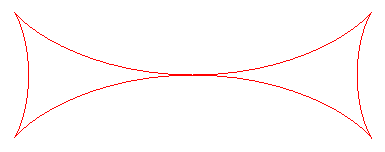
| Courbe étudiée par W. H. Besant en 1870, M. d'Ocagne en 1884, et W. Gaedecke en 1917. |
| Paramétrisation cartésienne : Équation cartésienne : Sextique rationnelle. Angle tangentiel cartésien : |
 |
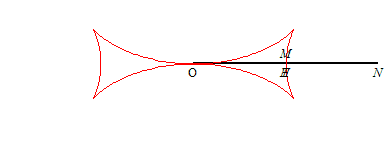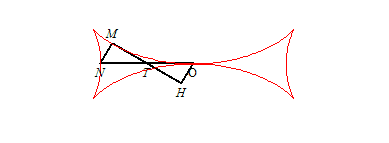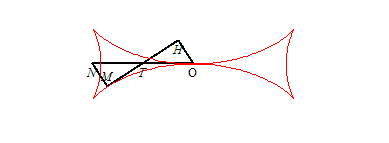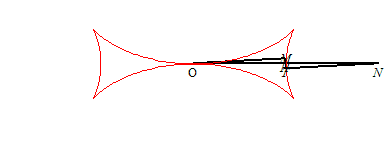
| La croix de Malte (que l'on devrait plutôt
dénommer demi-croix de Malte) est caractérisée
par le fait que le point T est le milieu du segment [ON],
(T étant le point d'intersection de la tangente avec
Ox,
et N celui de la normale - voir les
notations)
; ceci conduit à l'équation différentielle : Si H est le projeté de O sur la tangente, on a donc |
 |
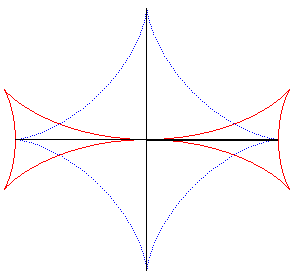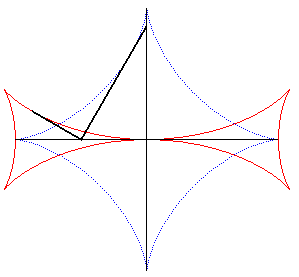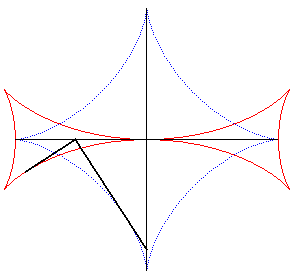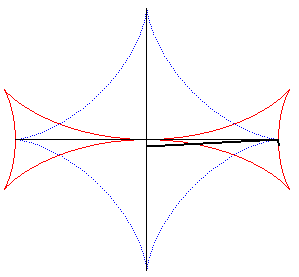
| La croix de Malte est l'enveloppe d'une perpendiculaire
à l'extrémité d'un segment de longueur constante dont
les extrémités se déplacent sur deux droites perpendiculaires
(le segment enveloppant, lui, une astroïde).
Voici cette propriété énoncée
en 1884 dans les Nouvelles Annales de Mathématiques p. 559 :
|
 |
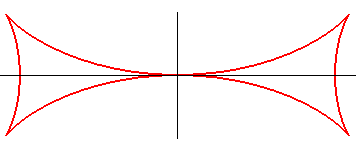
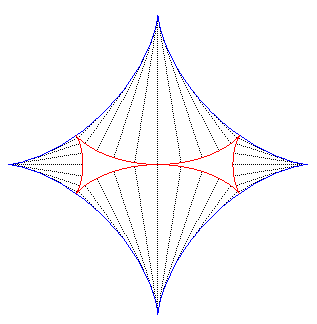
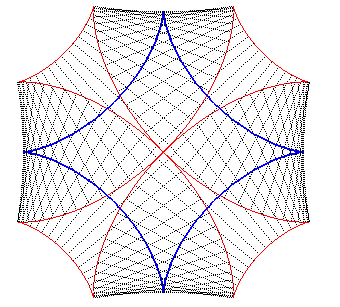
| La croix de Malte est aussi l'une des développantes
de l'astroïde (figure de gauche),
donc également l'une de ses courbes parallèles (figure de droite). |
  |
| La podaire de la croix de Malte par rapport à son centre est l'oeuf double. | 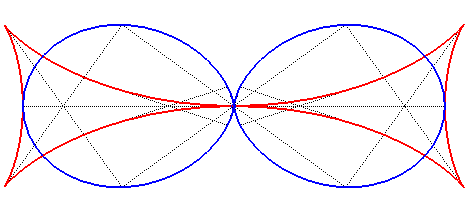 |
Sa courbe orthoptique est la cornoïde.
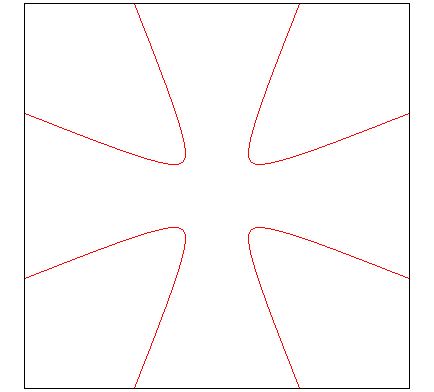
Mais une croix de Malte bien plus ressemblante a été
trouvée par [Cundy
et Rollet p. 71) :
| Équation polaire : Équation cartésienne : Quartique de genre 2. |
 |

Une croix de Malte non mathématique... |

...et une broderie à partir de la croix de Malte (première forme) réalisée par Daniel Alexis |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018