Sigmoïde : ayant la forme d'un sigma.

Une (courbe) sigmoïde est une courbe ayant, non la forme d'un S, mais plutôt celle d'un S étiré. Plus précisément : courbe située entre deux asymptotes parallèles possèdant un point d'inflexion, qui est aussi centre de symétrie, situé à égale distance des deux asymptotes.

Exemples de sigmoïdes normalisées de sorte qu'elles soient courbes d'une fonction impaire f dérivable croissant de –1 à 1 sur les réels et vérifiant .
 

Fonction f	Commentaire	Tracé
	Correspond à une branche de la quartique puntiforme : .
	Raccordement de deux portions d'hyperboles : .
pour t > 0.	Généralisation des deux précédentes ; ci-contre, animation pour t allant de 0,2 à 8.
	Tangentoïde hyperbolique.
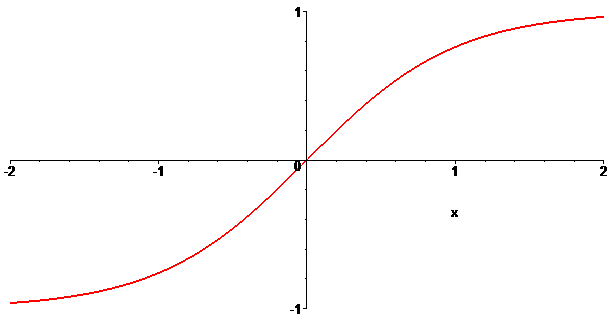	Tangentoïde.

 
 

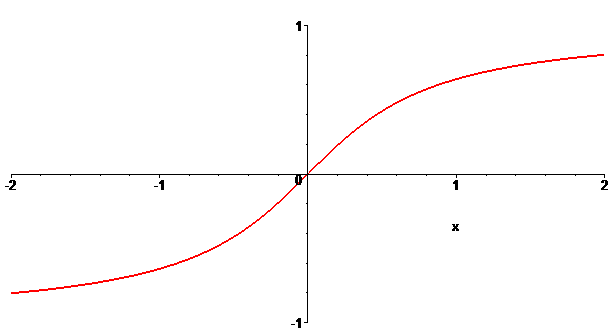courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023