Courbes étudiées par Pagani en 1825, La Gournerie en 1869, Pierre Nicaise en 2017. Le tore était appelé "speira" par les Grecs : spirique équivaut donc à torique. Autres noms : section torique, section annulaire. Site internet : www.lucamoroni.it/toric-sections/

 

Équation cartésienne réduite :  avec . Quartique bicirculaire.

Les spiriques planes sont les sections planes d'un tore ; pour obtenir tous les cas de l'équation cartésienne donnée en en-tête, le tore doit dans certains cas être considéré comme complexe.

Première résolution, avec un tore horizontal, plan incliné.
 

Pour un tore de centre O, d'axe Oz, de rayons majeurs et mineurs a et b, coupé par le plan situé à une distance d de O, faisant un angle  avec xOy et coupant xOy parallèlement à Ox, d'équation . Paramétrisation cartésienne dans l'espace : 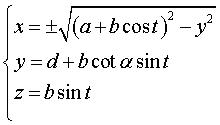 Ci-contre, exemple avec  et .
Paramétrisation cartésienne dans le plan, repère centré sur Oy :. Equation cartésienne correspondante : .

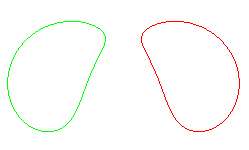Deuxième résolution, avec tore incliné et plan horizontal.
 

Le tore de centre O, de rayons majeurs et mineurs a et b, d'axe incliné dans le plan yOz d'un angle  par rapport à Oz ayant pour équation cartésienne : , sa section par le plan "z = d " a pour projection sur xOy la courbe d'équation : , ce qui donne l'équation :  , avec .

Les spiriques planes sont appelées spiriques «de Persée» quand le plan est parallèle à l’axe du tore ().
Lorsque le plan est bitangent au tore, on obtient un cercle de Villarceau du tore.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2020