Courbe de Talbot

COURBE DE TALBOT et généralisations
Talbot curve and generalization, Talbotsche Kurve und Verallgemeinerung

Courbe étudiée par Roche et Talbot en 1821, Tortolini en 1846, Dan Reznik et alii en 2020.

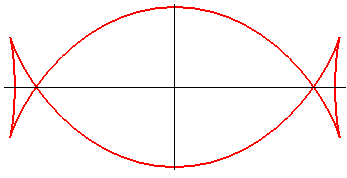Paramétrisation cartésienne, partant de l'ellipse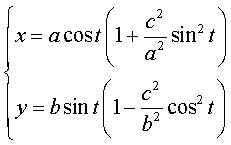

où

.
Sextique rationnelle.

La courbe de Talbot est l'antipodaire de l'ellipse par rapport à son centre. C'est donc l'enveloppe des droites perpendiculaires aux diamètres de l'ellipse à leurs deux extrémités.

pour la courbe a une forme ovale

pour la courbe a 4 points de rebroussements

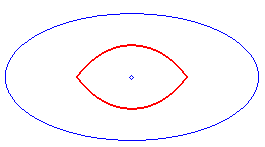La courbe de Talbot est donc aussi (à homothétie de rapport 1/2 près) la courbe isotèle de l'ellipse par rapport à son centre, soit le lieu des centres des cercles tangents à l'ellipse et passant par son centre. Sur cette île elliptique, la courbe de Talbot sans ses deux "nageoires" enserre la zone des points qui sont plus proches du centre que de la rive.

On peut généraliser cette courbe en considérant l'antipodaire de l'ellipse par rapport à un point quelconque de son grand axe, situé à d du centre.
On obtient la paramétrisation : . Dans les animations ci-dessous, la courbe rouge est l'isotèle de l'ellipse, donc image de l'antipodaire par une homothétie de rapport 1/2 de l'antipodaire.

Premier cas particulier : antipodaire de l'ellipse par rapport à un foyer (d = c).
La paramétrisation se simplifie en : .
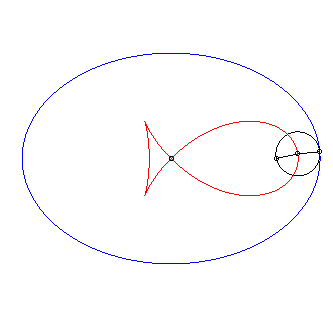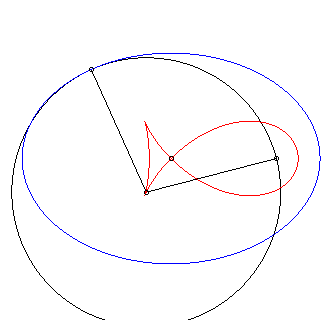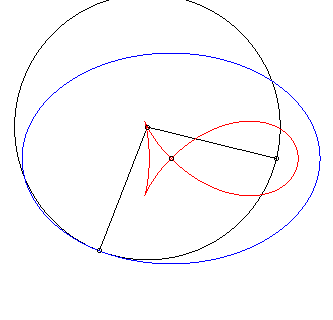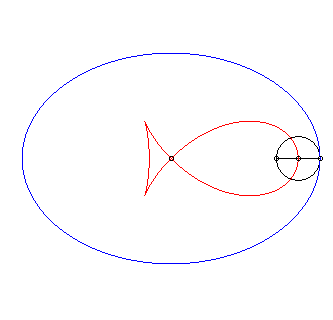
Le cas donne qui n'est autre, à dilatation près, que le poisson à nageoires pointues.
Isotèle de l'ellipse par rapport à un foyer.

Deuxième cas particulier : antipodaire de l'ellipse par rapport à un sommet principal (d = a).
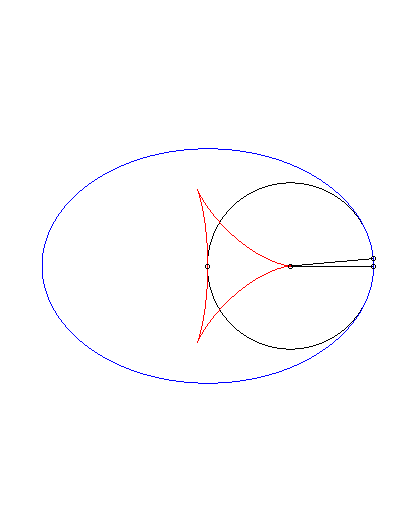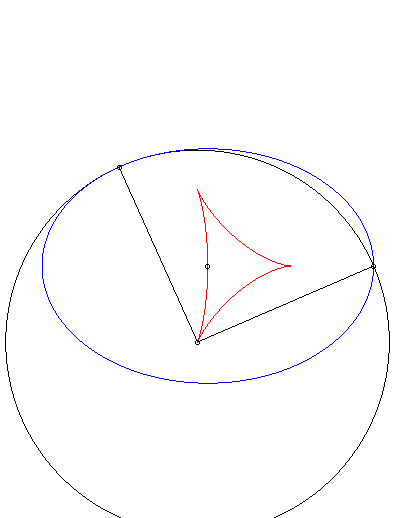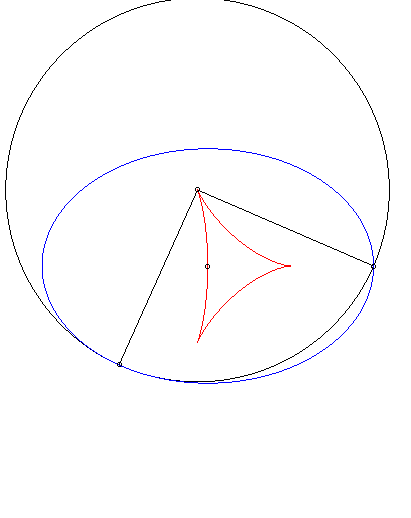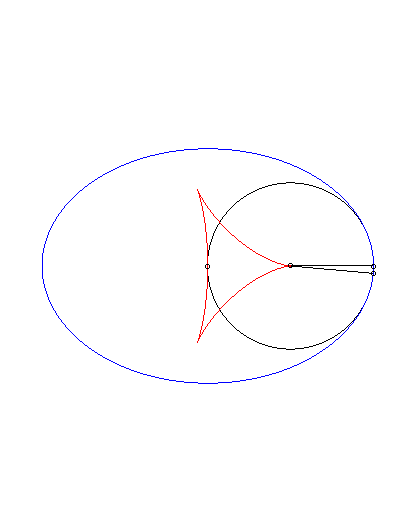
La paramétrisation se simplifie en : qui n'est autre, à dilatation près, que celle d'une deltoïde.
Isotèle de l'ellipse par rapport à un sommet principal.

Plus généralement, l'antipodaire de l'ellipse par rapport à un point de cette ellipse est l'image par une affinité d'une deltoïde, conservant de plus une aire constante égale à (voir lien Dan Reznik).
Paramétrisation : .
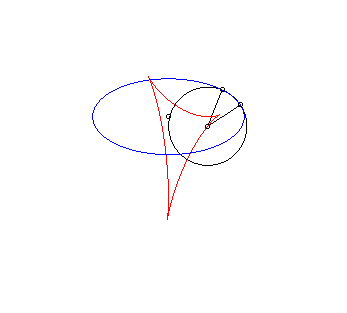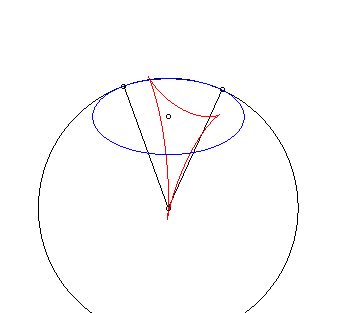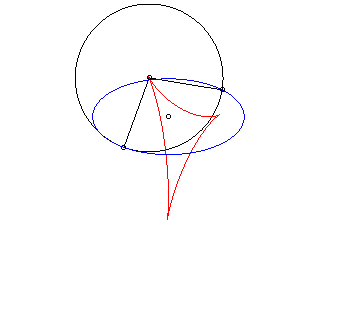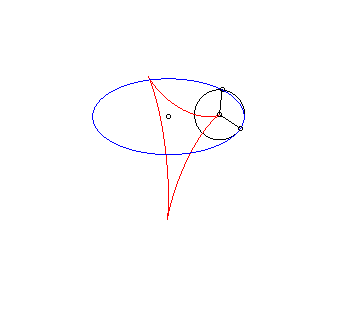
Isotèle de l'ellipse par rapport à un point d'icelle.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

On peut généraliser cette courbe en considérant l'antipodaire de l'ellipse par rapport à un point quelconque de son grand axe, situé à d du centre. On obtient la paramétrisation : .	Dans les animations ci-dessous, la courbe rouge est l'isotèle de l'ellipse, donc image de l'antipodaire par une homothétie de rapport 1/2 de l'antipodaire.
Premier cas particulier : antipodaire de l'ellipse par rapport à un foyer (d = c). La paramétrisation se simplifie en : . Le cas donne qui n'est autre, à dilatation près, que le poisson à nageoires pointues.	Isotèle de l'ellipse par rapport à un foyer.
Deuxième cas particulier : antipodaire de l'ellipse par rapport à un sommet principal (d = a). La paramétrisation se simplifie en : qui n'est autre, à dilatation près, que celle d'une deltoïde.	Isotèle de l'ellipse par rapport à un sommet principal.
Plus généralement, l'antipodaire de l'ellipse par rapport à un point de cette ellipse est l'image par une affinité d'une deltoïde, conservant de plus une aire constante égale à (voir lien Dan Reznik). Paramétrisation : .	Isotèle de l'ellipse par rapport à un point d'icelle.