Torpille

TORPILLE
Torpedo curve, Torpedo Kurve

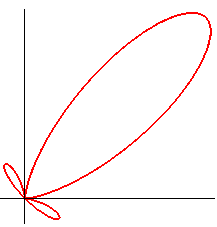
Courbe étudiée par G. Gohierre de Longchamps en 1884 (géométrie analytique, tome 2, 511-515).
Nom maison (G. de Longchamps dénommait cette courbe trifolium droit, nom qui désigne maintenant une famille plus générale).
Autre proposition : Moby Dick.

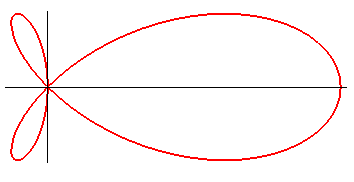
Équation polaire :

.
Équation cartésienne :

.
Paramétrisation cartésienne :

(

).
Paramétrisation complexe :

.
Quartique rationnelle.

Dans un repère tourné de p/4 :
Équation polaire : .
Équation cartésienne : .

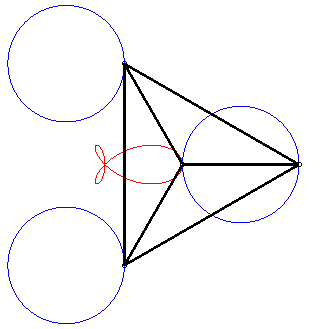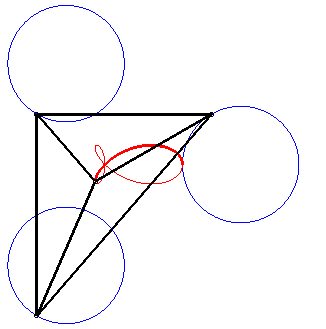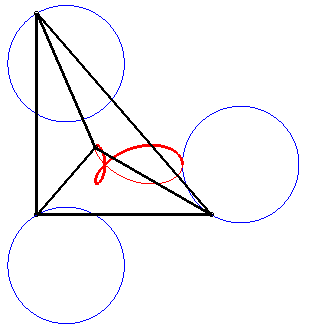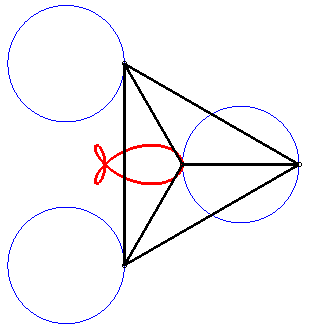
La torpille est la (courbe) strophoïdale d'un cercle (ici le cercle de centre (a/4, 0) passant par O) relativement à un point O du cercle et un point A situé à l'infini dans la direction du diamètre passant par O.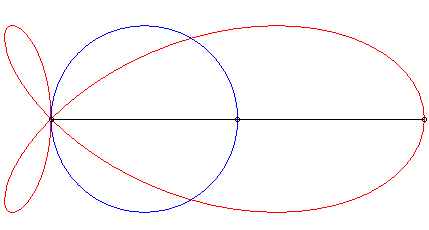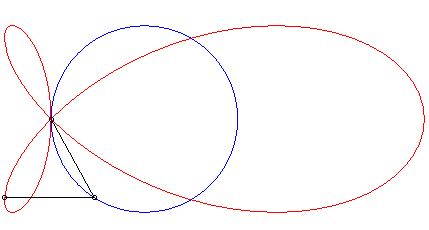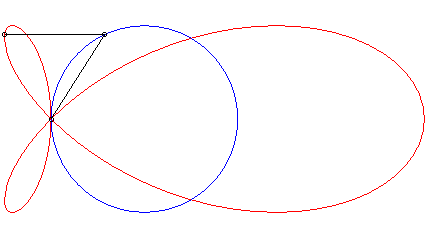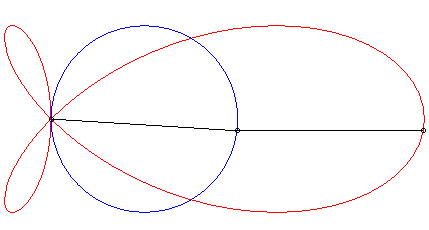
C'est aussi un cas particulier de trifolium droit (podaire de deltoïde par rapport au point du cercle inscrit symétrique d'un sommet de la deltoïde - voir à folium), de "poisson" et de tritrochoïde (cf la paramétrisation complexe). C'est le lieu de l'isobarycentre de 3 mouvements circulaires de mêmes rayons, deux étant de vitesses opposées, et le troisième de vitese double des 2 premiers.
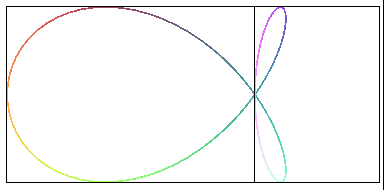
Comme tout "poisson" la torpille est une projection plane de la courbe de Viviani.

Elle s'obtient aussi comme orthopolaire de cercle.

Voir à trèfle équilatère une étude succinte de son inverse.

Une variante très proche de la torpille est dénommée "trifolium de Cramer" :

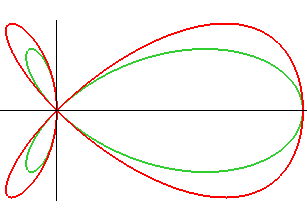Équation cartésienne : .
Équation polaire : .
Quartique rationnelle.

On se demandera bien pourquoi certains ont étudié des variantes de la torpille, et les ont dénommées "bitoïdes" :

bitoïde de Tardy

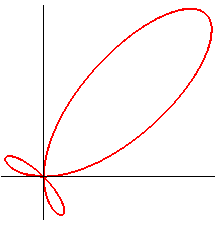courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres