
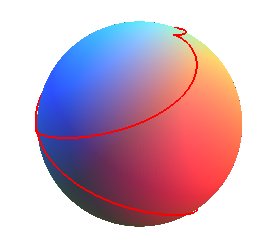
case q = 5/2, k » 0,56, slope » 75%

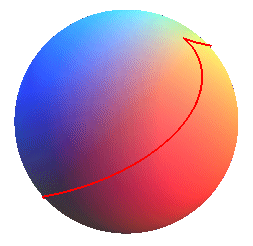
case q = 2/5, k » 0,17, slope » 25%
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SPHERICAL HELIX

case q = 5/2, k » 0,56, slope » 75% |

case q = 2/5, k » 0,17, slope » 25% |
| Notion studied by H.J. Jonas in 1905 and W. Blaschke.
See Loria 3d pp. 84 and 160. |
| Cartesian parametrization: i.e. |
The spherical helices are the helices, i.e. the curves with constant slope with respect to a given plane P, traced on a sphere.
It can be proved that they are the curves described by a point on a great circle of a sphere rolling without slipping on a fixed circle of the sphere, parallel to the plane P; therefore, they are special cases of spherical cycloids, as well as satellite curves; they have cuspidal points located on the fixed circle and its symmetrical image with respect to the center of the sphere.

| The second parametrization above shows that the projections
on the plane of the fixed circle are the epicycloids
with parameter q defined by |
 |
The spherical helices are also the involutes
of cones of revolution (loci of a point of a plane rolling without slipping
on the cone); the above helix is an involute of the cone of revolution
containing the two rolling circles.
| Do not mistake these curves for the rhumb lines, the tangents of which form a constant angle, not with a plane, but with the meridians. Do not mistake them either for the clelias. |
 Spherical helix with 10% slope; it looks like a rhumb line, but as opposed
to the latter, the extreme points are not asymptotic points.
|
See also the curves of constant
precession, the indicatrices of curvature of which are spherical helices.
  |
  |
| Model of spherical helix obtained as an involute of a cone.
It is a helix that makes one turn between two cuspidal points, therefore it is the case q = 1 (the horizontal projection is a cardioid); hence: circle at the summit with radius R/3, slope |
This staircase on a storage sphere has constant-size steps, and therefore
follows a spherical helix.
It is a helix that makes a half-turn between two cuspidal points, therefore it is the case q = 2 (the horizontal projection is a nephroid); hence: circle at the summit with radius R/2, slope |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018