Pavage de Durer

PAVAGE DE DÜRER
Durer's tiling, Dürersche Parkettierung

Pavage imaginé par Dürer en 1525 (Instructions sur la manière de mesurer, Livre II).
Albert Dürer (1471-1528) : théoricien de l'art et de la géométrie allemand.

Un programme maple de tracé:
restart:with(plots):
rotation:=proc(L,angle,vect) local rot: rot:=x->(x+vect)*exp(I*angle); map(rot,L): end:
N:=5:a:=Pi/N:
piece:=[0,exp(-I*a),exp(-I*a)+1,exp(-I*a)+1+exp(I*a),exp(I*a)+1,exp(I*a),0]:
Piece:=proc(n,k,m) rotation(piece,2*m*a+Pi/10,n+k*exp(I*a)+(n-k)*exp(-I*a)) end:
Piece2:=proc(n,k,m) rotation(piece,2*m*a+a+Pi/10,n+1+k*exp(I*a)+(n-k)*exp(-I*a)) end:
nn:=1:
display(seq(seq(seq(complexplot(Piece(n,k,m),color=red),k=0..n),n=0..nn),m=0..N-1),seq(seq(seq(complexplot(Piece2(n,k,m),color=red),k=0..n),n=0..nn),m=0..N-1),scaling=constrained,axes=none);

Le pavage de Dürer est un exemple de pavage polygonal monoédrique non périodique (en ce sens qu'il ne possède pas de symétrie de translation). Il possède par contre une symétrie de rotation (pavage radial), que n'a pas le pavage non périodique de Penrose.
D'autre part, un voisinage du centre du pavage de Dürer ne se retrouve nulle par ailleurs, contrairement à la quasi-périodicité du pavage de Penrose (tout motif se retrouve une infinité de fois).

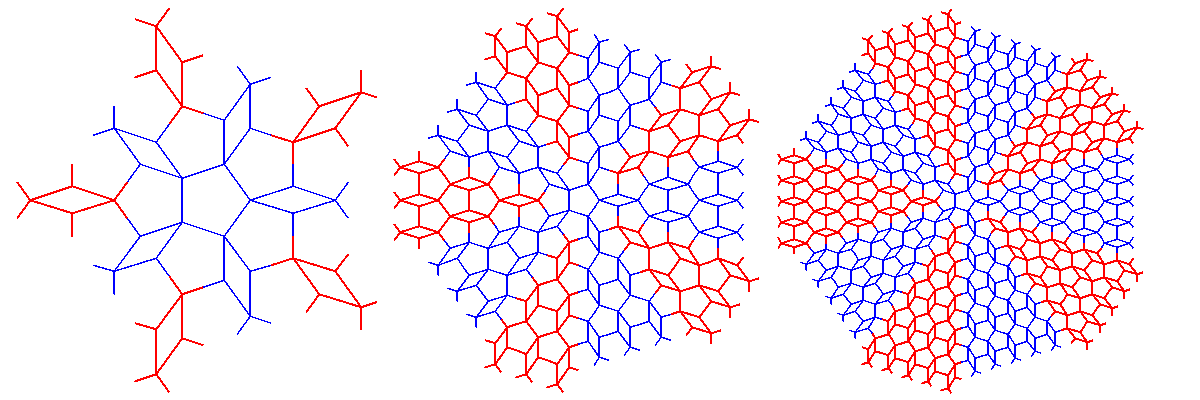
La pièce de base simplifiée du pavage de Dürer est un hexagone à symétrie centrale à deux angles de et 4 angles de (n = 5 pour Dürer). Cet hexagone pourrait paver le plan par translations, mais on peut aussi le faire paver par rotations d'angle comme indiqué ci-contre.
La figure de droite montre comment le pavage est constitué de 2n motifs formés de 1,2,3,...etc. pièces de base.
Il contient donc des plages aussi grandes qu'on veut du pavage par translation obtenu avec la même pièce de base.

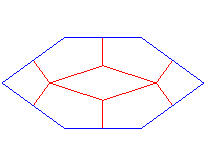
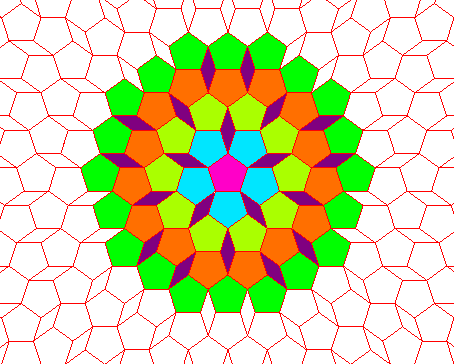
Si maintenant, uniquement dans le cas n=5, on remplace la pièce de base en bleu ci-contre par le motif dessiné en rouge, on obtient le pavage de Dürer originel, formé de deux pièces de base : un pentagone régulier, et un losange de petit angle .

S'il s'agit juste d'obtenir un exemple de pavage monoèdrique sans invariance par translation (mais présentant une symétrie de rotation), on peut utiliser le pavage ci-contre par des losanges de petit angle

(idée d'Alain Esculier).

Ci-contre, pavage périodique obtenu avec le pentagone et le losange de Dürer.

Type cristallographique : pmm (axes de symétrie orthogonaux).

Variante de type cristallographique : p2 (centres de symétrie).

Des variantes, par Alain Esculier

polyèdre suivant polyèdre précédent courbes 2D courbes 3D surfaces fractals polyèdres

La pièce de base simplifiée du pavage de Dürer est un hexagone à symétrie centrale à deux angles de et 4 angles de (n = 5 pour Dürer). Cet hexagone pourrait paver le plan par translations, mais on peut aussi le faire paver par rotations d'angle comme indiqué ci-contre. La figure de droite montre comment le pavage est constitué de 2n motifs formés de 1,2,3,...etc. pièces de base. Il contient donc des plages aussi grandes qu'on veut du pavage par translation obtenu avec la même pièce de base.
Si maintenant, uniquement dans le cas n=5, on remplace la pièce de base en bleu ci-contre par le motif dessiné en rouge, on obtient le pavage de Dürer originel, formé de deux pièces de base : un pentagone régulier, et un losange de petit angle .