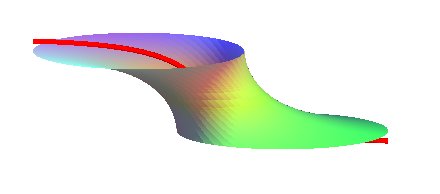
Cartesian parametrization:  (giving, for u 1, the part located in the half-space z  0). Horizontal circles with radius u centered on  (red curve above). Nota: the integrals above can be computed thanks to elliptic functions.

The skew catenoid with equation given above is the solution to the problem that consists in finding the circledminimal surfaces. Note that the circles are therefore, necessarily, parallel to one another, and the line composed of the centers of the circles is traced on a plane perpendicular to the planes of the circles.
The skew catenoid provides also a solution to the Plateau problem that consists in finding a minimal surface joining two circles located in parallel planes (but note that there are some conditions on the circles for the surface to exist - start by considering the case of coaxial circles at catenoid).

If we take k = 0 in the above formulas, we get the classic right catenoid.
 
 

The surface is located between the two planes  and is asymptotic to these two planes  (). Thanks to translations of the previous pattern and adjustments of the asymptotic half-planes, we get a periodic smooth minimal surface, called Riemann's minimal surface. All the sections by horizontal planes are circles or lines.

Image taken from Wikipedia

See also the finite Riemann minimal surface.
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017