ROTOID
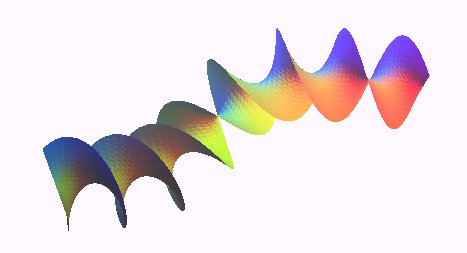
Closed normal ruled rotoid with a horopter
curve as bore
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ROTOID

Closed normal ruled rotoid with a horopter
curve as bore
| Other name: generalized helicoid.
Alain Esculier's website. |
| For a spine curve where h is the reduced shift of the rotoid and 2ph its shift. |
The word rotoid refers to any surface generated
by a regular screw of a curve (the generatrix) around a fixed curve (the
"spine curve, or "bore" of the rotoid).
The intersection between the rotoid and a tube with same
spine curve is a union of solenoids
with reduced shift h.
When h is positive, the rotoid is said to be right-handed,
and left-handed otherwise.
When the spine curve is linear, we get the helicoids.
When the generatrix is a line, we get the ruled rotoids, with similar definitions as those of the ruled helicoids.
The Möbius surface is a closed normal ruled rotoid with a circle as its spine curve.
When the center of a regular polygon moves along a curve,
perpendicularly to it, with a regular torsion motion, the sides of the
polygon trace a surface that we will call "rotoidal prism". Each "face"
of this "prism" is a portion of open normal ruled rotoid.
For the case of a linear spine curve, see at ruled
helicoid.
For the case of a circular spine curve, a (convex) polygon
with n sides, and a torsion of k n-ths of a turn for
one revolution, we get a surface composed of d = GCD(n, k)
"faces" (after a revolution, the side #x of the polygon connects
with the side #x+k modulo n). Moreover, there are also d
"edges", which form a toroidal
link of type (k, n): each component turns n/d
times around the axis, and winds k/d times around the torus.
In particular, if n and k are coprime,
the rotoidal prism has only one "face" and only one edge.
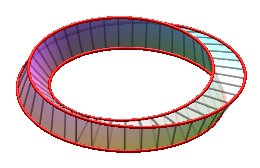
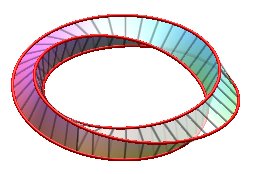
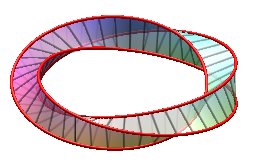
Examples for n = 3:
| k = 1: one face, one untied edge | k = 2: one face, one edge tied as a trefoil knot | k = 3: three faces (fake Möbius strips with 2 half-twists), three edges (Villarceau circles of the torus, fake Borromean rings) | k = 4: one face, one edge, toroidal knot of the type (4,3), prime knot with 8 crossings. |
 |
 |
 |
 |
Examples for n = 4:
| k = 1: one face, one untied edge | k = 2: two faces, two untied edges, forming a Salomon knot | k = 3: one face, on edge, toroidal knot of type (3,4), prime knot with 8 crossings. | k = 4: 4 faces (fake Möbius strips with 4 half-twists), 4 edges (Villarceau circles) |
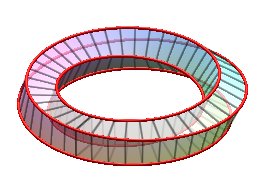
Was named monohedron by Jean-Pierre Petit |
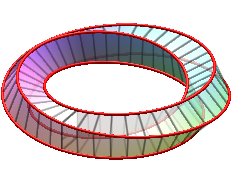 |
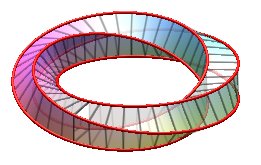 |
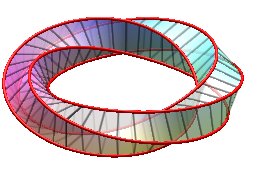 |
Examples for n = 6:
| k = 1: one face, one untied edge | k = 2: two faces, two untied edges | k = 3: three faces, three edges, toroidal link of type (3,6). | k = 4: two faces, two untied edges, toroidal link of type (4,6). |
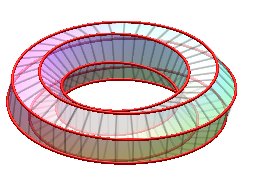 |
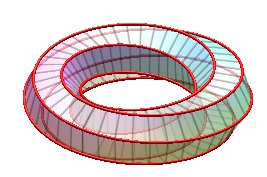 |
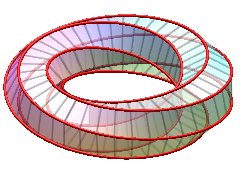 |
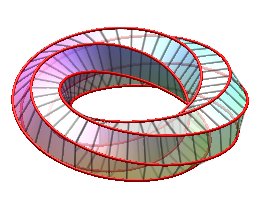 |
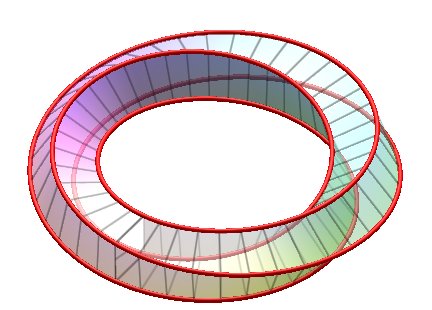 |
Opposite, a view of the case n = 4, k =
2; if the tracing square is contracted into a segment line, (in other words,
if we stick two edges together), we get a Möbius
strip.
Therefore, this solid can also be seen as a Möbius strip cut in thick cardboard, the length of the strip being equal to the width of the cardboard. |
| Generalization to the case where k is a rational
number p/q.
The linear section of the resulting surface is composed of q polygons with n sides, i.e. a polygram with symbol {qn/q}. Opposite, the case n = 3, p =1, q =2. |
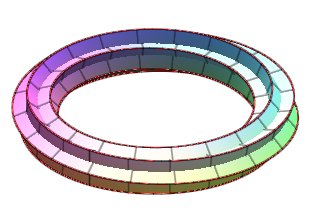  |
Game: find the values of n and k in the
sculptures below:
 |
|
 |
 |
| Work photographed in the Mentoring Museum of Tours | Work by Jean-Daniel Huyghe | Work by Christophe Chini |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017