Conic

CONIC

Curve studied by Menechme in 400 BC then by Archimedes, Apollonius, Kepler etc...
Abbreviation of "conical section".

General Cartesian equation:

, non-degenerate (or possibly empty) if the associated homogeneous form

is non-degenerate.
Cartesian and polar equations in a frame with origin a vertex and focal axis the abscissa:

.
Polar equation in a frame with origin a focus and focal axis the abscissa:

; polar equation of the corresponding directrix:

.
Case of centred conics, in a frame with origin the centre and focal axis the abscissa:
Cartesian equation:

, i.e.

.
Polar equation:

The current definition of a conic is an algebraic curve of degree two.
This definition includes the degenerate cases (in the Euclidian plane: empty set, point, union of two lines) and enables the statement that conics are the planar sections of the quadrics.
Nonetheless, in this website, the word conic refers only to the non-degenerate cases: the ellipse, parabola, hyperbola.

With this convention, here are the various geometric definitions of conics:
1) Definition of the Greeks.
The conics are the sections of a cone of revolution by a plane not passing by its vertex.

Ellipse
Parabola
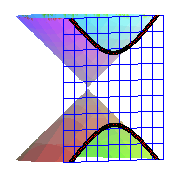
Hyperbola

The "perfect compass", invented by a Persian mathematician of the 10th century, allows to draw (portions of) conics using this definition.
The arm SM rotates around the axis SO while maintaining a constant angle and thus describes a cone of revolution with symmetry axis SO. Therefore, the point M traces a conic on the plate.
The rose generatrix, symmetrical image of SM about the axis, obviously intersects with the plate on the right, so the curve traced is a hyperbola.
Opposite model made by Olivia De Cocq and Darwin Libioulle, students of Ecole polytechnique de Bruxelles.

2) Definition with focus and directrix.

The conics are either circles, or the loci of points for which the ratio of the distances to a fixed point (the focus F) and to a fixed line (the directrix (D)) is constant (equal to the eccentricity e); the ellipses are obtained for e < 1, the parabola for e = 1, the hyperbolas for e > 1.

It is only in 1822 that Dandelin linked these first two definitions, by showing that foci and directrices are obtained thanks to two inscribed spheres:

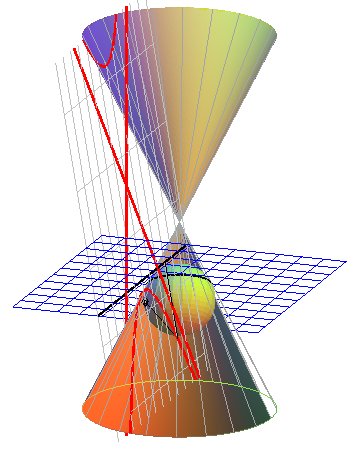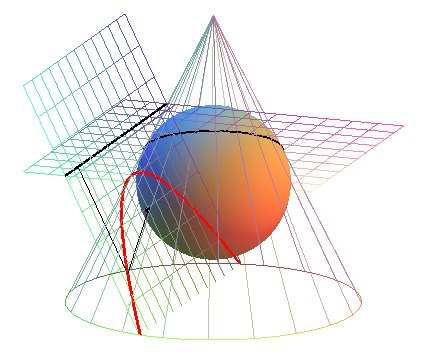3) Definition as an equidistance curve between a point and a generalised circle.
The conics are the loci of points equidistant to a fixed point (the focus) and a circle or a line (C) (the directrix line or circle), i.e. the isotel curves of the generalised circle; in other words, they are the loci of the centres of variable circles constrained to pass through a fixed point and to be tangent to (C).
When the focus is inside the circle, we get the ellipses, when it is outside the circle, the hyperbolas, and when (C) is a line, the parabola.

More generally, the loci of the centres of circles tangent to generalised circles with different radii are the reunions of two conics.

4) Definition as orthocaustic of a circle or a line.

The conics are the orthocaustics (or negative pedals) of a circle or a line (C') (the main circle or the tangent at the vertex).

When the light source, which also is the focus of the conic, is inside the circle, we get the ellipses, when it is outside, the hyperbolas, and when (C') is a line, the parabola.

Therefore, the conics are also the envelopes of the perpendicular bisector of a segment line joining a point to a circle or a line (the directrix circle or line) (in other words, they are the curves for which the orthotomic is a circle or a line).

5) The conics are also the anticaustics of lines.

The first definition has various implications in daily life: for example, the edge of the light trace created by a lampshade or a flashlight on a wall is a conic.

Elliptic shadow
Hyperbolic shadow

A perspective view of a circle is a conic; it is an ellipse, a parabola or a hyperbola depending on whether the observer is outside, on the perimeter, or outside the circle.

An observer located at the point (0, - d, h) looks at the unit circle: when they get closer to the circle, they first see an ellipse with major axis parallel to Ox, then a circle (when d² = h² + 1), then an ellipse with major axis parallel to Oy, then a portion of parabola (when d = 1), and finally a portion of hyperbola.

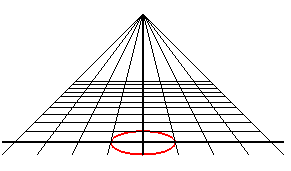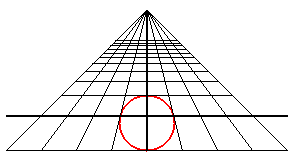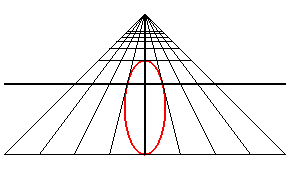
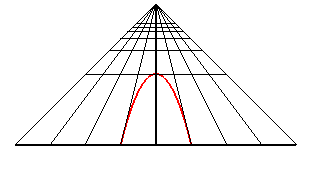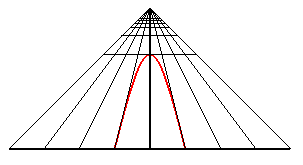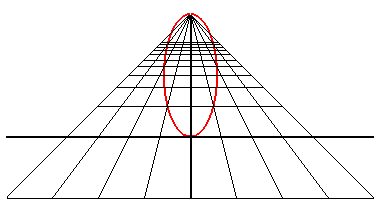Conversely, an observer looking at the parabola y = x² sees an ellipse!

Photo d'Andreas Gurski In this circular theatre, the perspective of the tiers, for a spectator located on one of them, are parabolas.

In fact, from a projective point of view, there only exists one conic, in the sense that all conics are images of another one of them by a homography.

The trajectory of a particle subject to a force centred on F and proportional to 1/MF² is a conic with focus F:

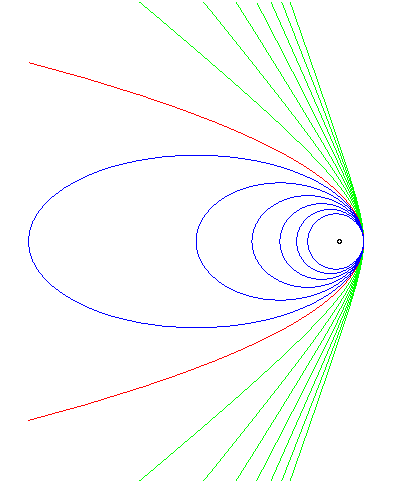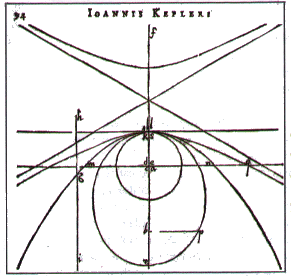
The same figure, from Kepler's hand

The trajectory of a boat B, moving in a current with constant speed e.v, itself with a constant speed v, in such a way that its axis is always perpendicular to the line BP, where P is a fixed lighthouse, is a conic with focus P, eccentricity e and focal axis parallel to the current: in a frame where Px is parallel to the current. Therefore, it is an ellipse if the speed of the boat is greater than that of the current, a parabola if they are equal, a hyperbola if it is less than that of the current. In fact, the movement has a 1/BP² central acceleration, exactly like the particle above.
(with the same idea, see the curve of the swimmer).

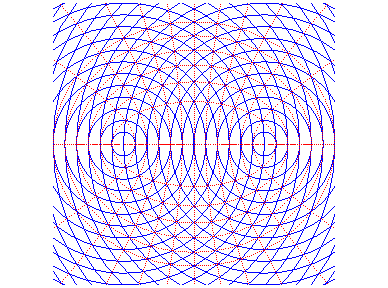
When two circular waves emitted by F and F' meet, the amplitude is proportional to the distances to F and F', and the phase is proportional to the sum of these distances. Hence these interference patterns, composed of an orthogonal lattice of ellipses and hyperbolas:

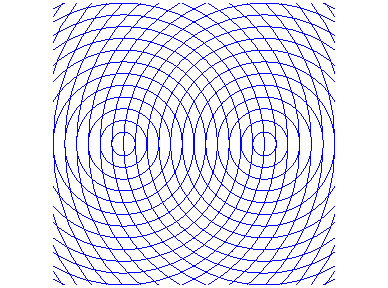
The inverses of conics are the rational circular cubics when the centre of inversion is on the conic, and the rational bicircular quartics otherwise.