Cornu spiral

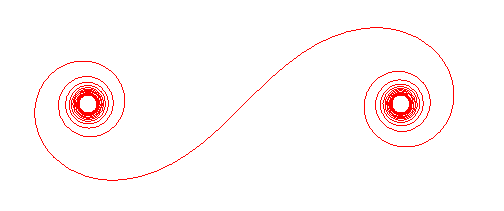
CORNU SPIRAL OR CLOTHOID

Curve studied by Jacques Bernoulli in 1705, Euler in 1743, Fresnel in 1818, Cornu in 1874, Cesaro in 1886 (who gave it the name clothoid).
Other names: Euler spiral, Fresnel spiral, volute spiral, arc radioid.
In German: Spinnlinie.
Alfred Cornu (1841-1902): French physicist.
Clothoid comes from the Greek klothein: spin (wool), the shape of the curve reminds of the shape of the thread wrapping itself around the weaving loom. Clotho was the one of the three Parcae who spun human beings' destiny. There is no link with the English word cloth.
Transcendental curve.

Kinematic definition:

(2 among these three equations are enough).
Cartesian parametrization:

Complex parametrization:

.
Transcendental curve.
Cartesian tangential angle:

.
Curvilinear abscissa: s = a t.
Radius of curvature:

.
Intrinsic equation 1:

.
Intrinsic equation 2:

.
The asymptotic points

and

can be determined thanks to the Fresnel integrals

The Cornu spiral, or clothoid, can be defined as the planar curve for which the curvature is proportional to the curvilinear abscissa.
Since the distance between two points on the curve is , this curve, once it was traced, gave (before the modern computational abilities) approximate values of this integral, that appeared in calculations of the resulting vibration during diffraction phenomena; it is reason why this curve was used by the physicist Cornu.

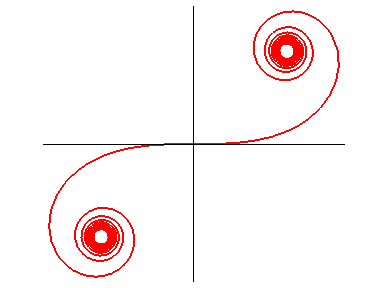
Kinematic definition: the clothoid is the curve for which, when it is travelled along at constant speed v, the curvature varies in proportion to time.
The angle of rotation of the steering wheel of a car is proportional to the angle of the wheels, which itself is equivalent, in a neighbourhood of 0, to the curvature multiplied by the distance between the front and back wheels of the car. Therefore, the clothoid approximates, in its central part, the curve described by a car driven at constant speed by a driver turning the wheel at constant speed. This curve is referred to as curve of constant gyration, hence its use in the tracing of curves of highways.

Furthermore, as any curve with a point of zero curvature, segments of lines and of clothoids can be connected in such a way that the curvature varies continuously along the curve. Therefore, the centrifugal force, to which is subject an observer travelling continuously along this curve, varies continuously, which is not the case for a connection circle-line, hence the use of clothoids for railway tracks too. These curves are, more generally, referred to as radioids (hence the name arc radioid given to the clothoid).

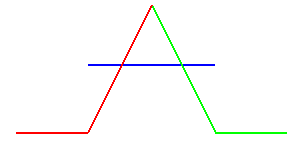
Two orthogonal segments of lines, connected to one another by an arc of a circle (blue curve) on the one hand, two arcs of clothoids one the second hand. The ratio of the two length is .

Plot (corresponding to the previous diagram) of the curvature against the curvilinear abscissa. It can be noted that for the arcs of clothoids, it is continuous (but not differentiable) along the whole trajectory.

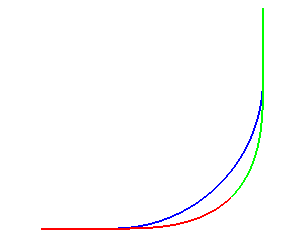
The clothoid also appears in the problem of determining the shortest trajectory joining two points on the plane, with a bounded derivative of the curvature, given tangents and curvatures at the beginning and the end, and continuous tangent and curvature. The optimal trajectory is an arc of a clothoid or a segment of a line.

The Mannheim curve of the clothoid is a rectangular hyperbola and its radial curve a lituus.

A generalisation of the clothoid is the curve for which the curvature is proportional to the n-th power of the curvilinear abscissa (the classic clothoid being the case n = 1). It is studied under the name pseudo-spiral of Pirondini (opposite, the case n = 2); it so happens that the evolute of the clothoid is a pseudo-spiral of index n = -3).
Other generalisation: case where the curvature is a polynomial in s.

See also the anti-clothoid, which is none other than the involute of a circle.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra