Maltese cross

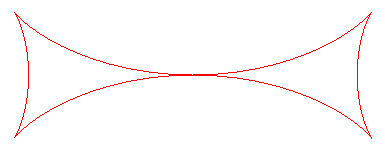
MALTESE CROSS

Curve studied by W. H. Besant in 1870, M. d'Ocagne in 1884, and W. Gaedecke in 1917.
Other name : bow tie.

Cartesian parametrization:

.
Cartesian equation:

.
Rational sextic.
Cartesian parametrization in a frame turned by p/4:

(

).
Length:

; Area:

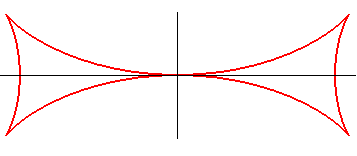The Maltese cross (that should rather be called half of a Maltese cross) is characterized by the fact that the point T is the middle of the segment line [ON] (T being the intersection point between the tangent and Ox, N the one between the normal and Ox - see the notations); this leads to the differential equation:

.
If H is the projection of O on the tangent, then

, and T is the middle of [MH].

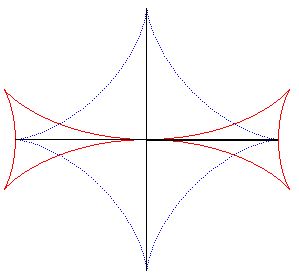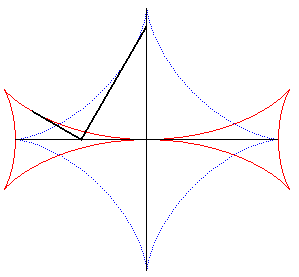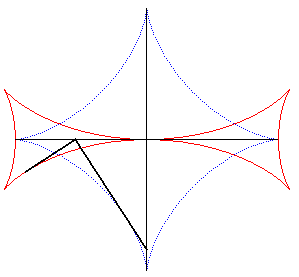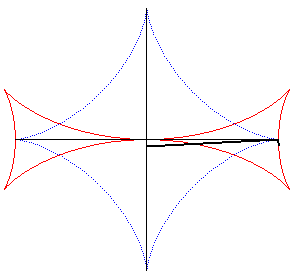
The Maltese cross is the envelope of a line perpendicular at the extremity to a segment line of constant length the ends of which move on two perpendicular lines (the enveloping segment is an astroid).

See this property stated in 1884 in the Nouvelles Annales de Mathématiques p. 559:
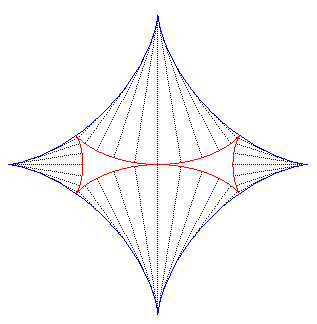
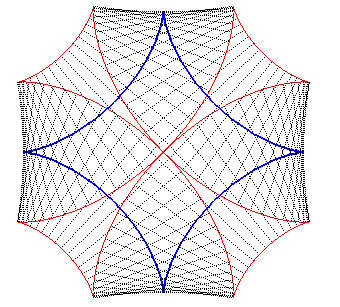
"if one of the sides of a right angle has a constant length and slides between two rectangular axes, then the other side envelopes the Maltese cross".

The Maltese cross is also one of the involutes of the astroid (figure on the left),

and, therefore, one of its parallel curves (figure on the right).

The pedal of the Maltese cross with respect to its centre is the double egg.

Its orthoptic curve is the cornoid.

A non-mathematical Maltese cross...

...and an embroidery from a Maltese cross designed by Daniel Alexis

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra