Pursuit curve

PURSUIT CURVE
Le chien court deux fois plus vite que le lièvre

Curve studied by Leonardo da Vinci and Pierre Bouguer in 1732, Du Boisaymé in 1811, Dunoyer in 1906, and Morley in 1921 (circular case).
Other name: dog curve.

Vectorial differential equation:

, that translates into the differential system:

, or

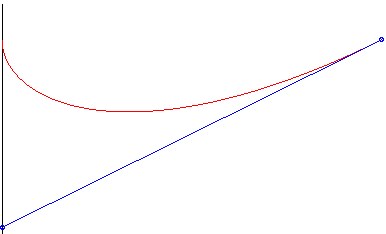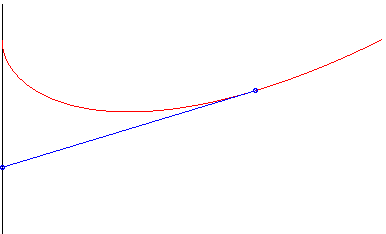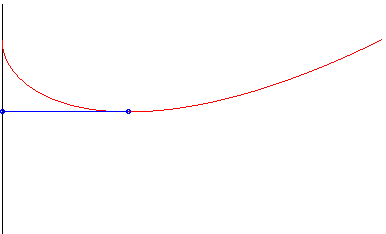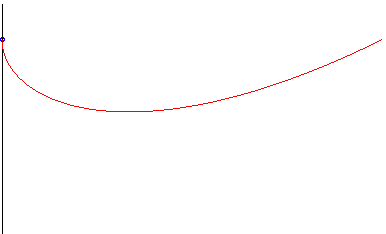
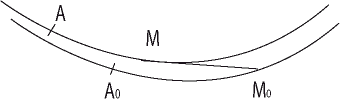
The notion of pursuit curve refers to the trajectory of a moving point M (the dog or the chasing plane) the movement of which is, at every instant, oriented in the direction of another moving point M₀ (the hare, or the chased plane), the trajectory of which is called escape curve. In general, movements of M and M₀ are considered to be uniform, with speeds V and V₀= kV.
Given the trajectory of M₀, the trajectory of M is defined in this case by the fact that (MM₀ ) is tangent at M to its trajectory, and the curvilinear abscissa of M is proportional to that of M₀:

As one might expect, the dog catches the hare with certainty if and only if it runs faster than it (k < 1). When the two speeds are equal, then the distance between the dog and the hare tends to a constant a, and the curve of the dog tends to become the tractory of that of the hare with a leash of length a.

I) Simplest case: the escape curve is linear.

The hare describes Oy at speed V, and the dog chases it at speed V/k.

If the coordinates of the dog are (x, y), then the data translates into the equations:

which provide the differential equation of the trajectory of the dog: , i.e.

If the dog is at A with coordinates (a, b) when the hare is at O, then the first integral is: where with

and we get the curve with equation:
with if k ¹ 1
and if k = 1

and the kinematic equation is given by: if k ¹ 1
if k = 1.

The curve is algebraic iff k is rational: if k = p/q with p and q coprime, then the degree is 2p when k > 1 and p + q when k < 1.

In particular, when k = 1/2, we get a half-Tschirnhausen cubic (complete equation: ).

The dog catches the hare iff k < 1, and it catches it at (0, b - f(a)), i.e. if b = 0.
When k = 1, the distance between the dog and the hare goes to a constant, equal to c/2.

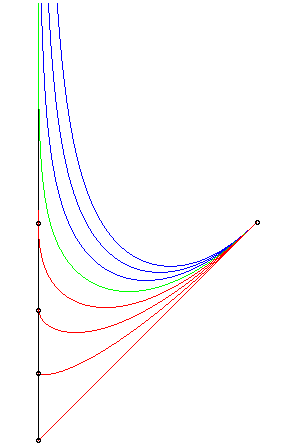
in red: the dog runs faster than the hare: it catches it.
in green: it runs as fast: no catch possible, and in blue, even less...

The dog has the same speed as the hare: their distance goes to a constant.

Note that if the dog were intelligent and ran in a straight line with anticipation, it could catch the hare iff (for b > 0) and therefore could always catch it if it ran just as fast.

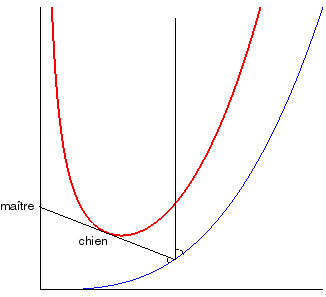
The dog curve for is the caustic by reflection for vertical incident rays of the generalised parabola with ; opposite, the case k = 2 (cubical parabola).
In the case k = 1, the dog curve is the caustic by reflection for vertical incident rays of a logarithmic curve.

See also the anallagmatic spirals, which are the wheels associated to these pursuit curves.

II) Case of a circular escape curve (that is said to have been solved only in 1921).
For the circle with centre O and radius R, we get the differential system: that enables us to trace the curves thanks to some software.

The dog catches up with its master again iff k < 1; when k = 1, the distance dog-master goes to 0, but it does not catch up with them; and when k ³ 1, the curve has the circle with centre O and radius R/k as an asymptotic circle, and the distance dog-master goes to .

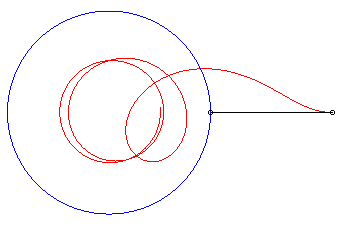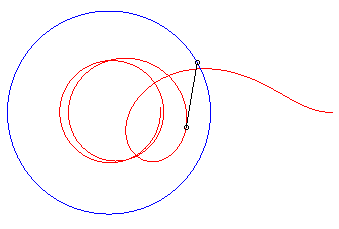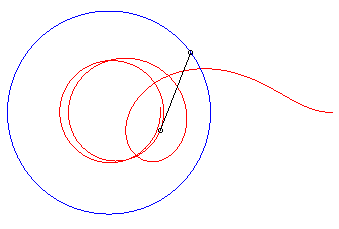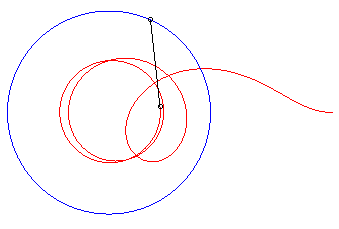Vdog = 2 Vmaster: the dog catches up with the master. Vdog = Vmaster: the dog catches up with the master... at infinity. Vdog = 1/2 Vmaster: the distance from the dog to the master goes to and it ends up turning around a circle with radius R/2.

VARIATION (based on an idea of Alain Esculier): the speed of the dog is no longer proportional to that of the master, but to their distance.

Vectorial differential equation: , that translates into the differential system: .
Equations of motion for the dog: .

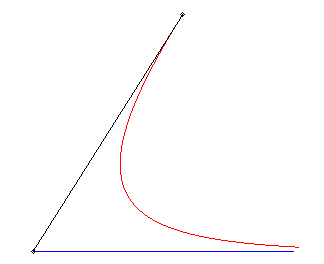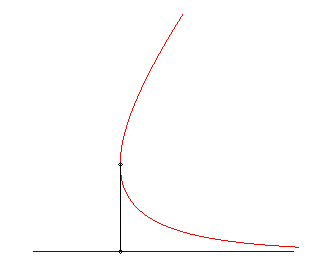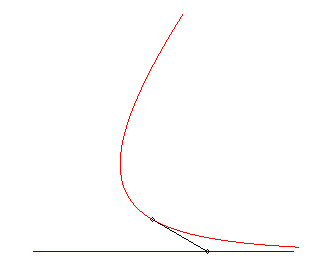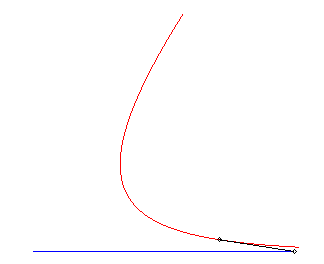
I) Linear escape curve

For a master (vt, 0), equations of motion for a dog passing by (0, b):
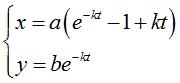(a = v/k).
Trajectory of the dog: .
The speed of the dog goes to that of the master, and their distance goes to v/k.

II) Circular escape curve.

For a master , equations of motion for a dog passing by (0, 0): .
The trajectory of the dog has the the circle with centre O and radius as its asymptote, its speed goes to , and its distance to the master goes to .

A generalisation consists in considering the pursuit curves when the velocity vector of the dog forms a constant angle with the line that joins it to the master; the simplest case is that where the master does not move: the dog follows a logarithmic spiral.
The case of a right angle is studied at Duporcq curve.

One can also consider 3D pursuit curves, and study pursuit systems.

For other curves travelled on by dogs, see the swimming dog curve (dog swimming against the current towards its master on the bank) or the conchoid (dog constantly pulling on its leash in the direction of a fixed point).
Compare to the shadowing curve.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

If the coordinates of the dog are (x, y), then the data translates into the equations:
which provide the differential equation of the trajectory of the dog:	, i.e.
If the dog is at A with coordinates (a, b) when the hare is at O, then the first integral is:	where with
and we get the curve with equation:	with if k ¹ 1 and if k = 1
and the kinematic equation is given by:	if k ¹ 1 if k = 1.


Vdog = 2 Vmaster: the dog catches up with the master.	Vdog = Vmaster: the dog catches up with the master... at infinity.	Vdog = 1/2 Vmaster: the distance from the dog to the master goes to and it ends up turning around a circle with radius R/2.