Curve studied and named by C. Masurel in 2013.

 

Polar equation:  ( n > 0) i.e. . Polar parametrization, for : . Polar tangential angle: . Curvilinear abscissa:  for , for n = 1 (coming from ).

The blue tangent at the intersection point with the reference circle is the line . Traced here for n = 2.

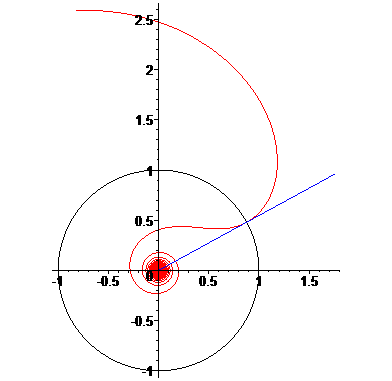
The anallagmatic spirals are the curves with the above polar equation.
As indicated by their name, and as proven by their equation, they are invariable under inversion (with pole O and square of the radius of inversion equal to a).
 

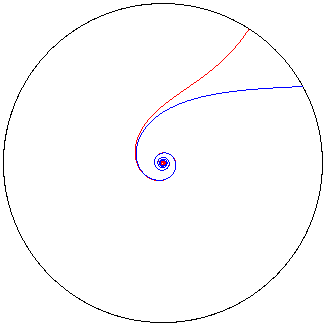
The branch outside the reference circle has an asymptote: the Archimedean spiral of index 1/n:

and the inside branch has an asymptote: the Archimedean spiral of index -1/n:

 

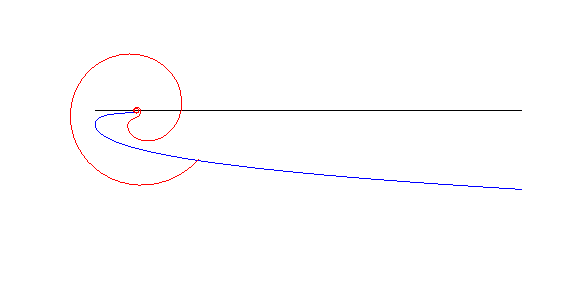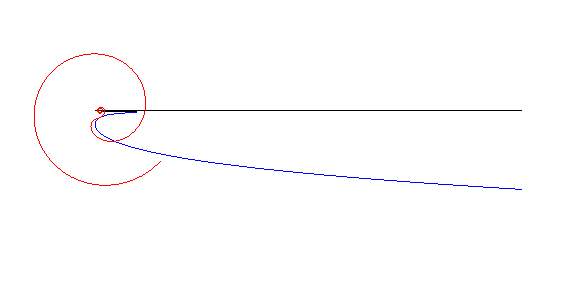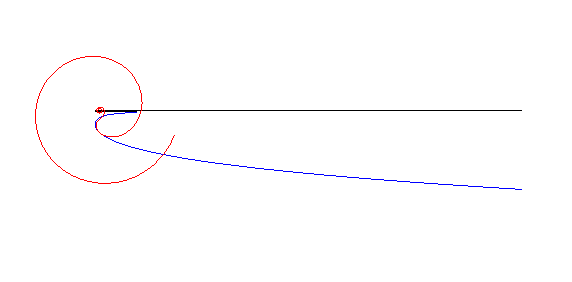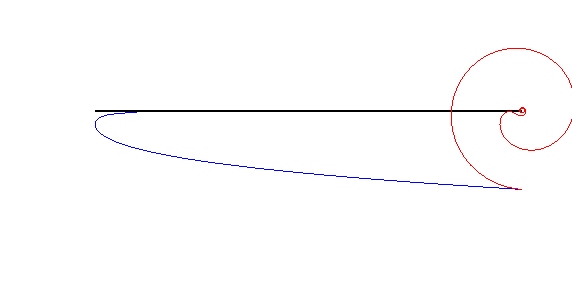
The anallagmatic spirals are the "wheel" associated to the linear pursuit curves (see wheel-road couple). More precisely, if an anallagmatic spiral with parameter n rolls, like in the opposite figure, on the pursuit curve with parameter n (= speed of the dog / speed of the master), then the pole of the spiral describes the asymptote (case n1) or the tangent at the vertex (case n < 1) of the pursuit curve.

 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017