PLÜCKER QUARTIC, AMPERSAND CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
PLÜCKER QUARTIC, AMPERSAND CURVE
| Curve studied by Plücker in 1839.
Julius Plücker (1801-1868): German mathematician and physicist. The name "ampersand curve" was given by [Cundy and Rolett]. Websites: perso.univ-rennes1.fr/christophe.ritzenthaler/cours/elliptic-curve-course.pdf (p. 43) library.msri.org/books/Book35/files/gray.pdf (p 122) |
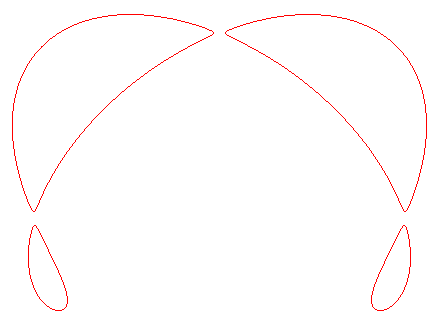
| In 1839, J. Plücker constructed a quartic
for which the 28 bitangents are real and distinct.
Equation:  .
The figure on the right shows the 4 lines |
 |
|
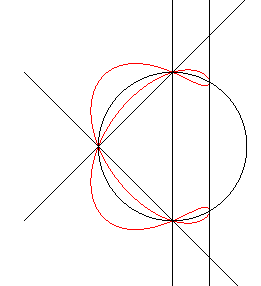For cte >0 small enough, the quartic has four components, each having a concave part, called "meniscus", each having a bitangent; added to the 6 times 4 = 24 bitangents linking two components, this indeed makes 28 bitangents in total. |
 |
See the Salmon quartic
for a simpler curve with 28 bitangents.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
,
and the circle 
that were used to determine this curve, as well as the curve in the case
where the constant is zero (rational quartic with 3 double points). It
is this curve that Cundy and Rolett call "ampersand curve".