TRIFOLIUM
| next curve | previous curve | 2Dácurves | 3D curves | surfaces | fractals | polyhedra |
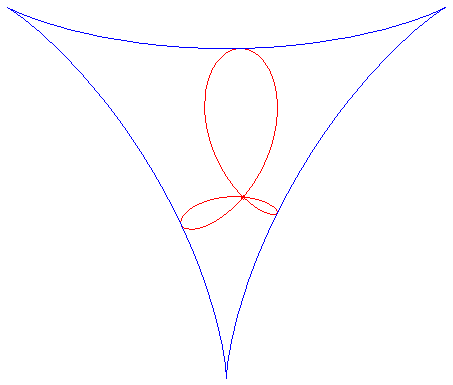
TRIFOLIUM

| Curve studied by G. de Longchamps in
1887 (journal de mathématiques spéciales
p. 203) and Brocard in 1891 (journal
de mathématiques spéciales p 32).
Trifolium (Latin): trefoil. |
| Polar equation: Cartesian equation: Rational quartic. |
The trifolia are the pedals of the deltoid with respect to a point inside the deltoid; therefore, they are special case of folia.
Here, the pole of the pedal is the point O, the centre of the deltoid is A(a, b) and its cuspidal point is B(a3r, ľb) (the deltoid is parametrized by: ); when A is on O, we get the regular trifolium.
They are the curves composed of three leaves joining at a triple point.
Two of the three tangents at the point are orthogonal when the point with respect to which the pedal is taken is located on the orthoptic of the deltoid, which is its inscribed circle.
With and
, we get these special trifolia:
| Polar equation: Cartesian equation in the frame corresponding to |
Furthermore, these special cases are strophoids of a circle with a pole located on the circle and a point A located at infinity; see for example the torpedo, special case of a right trifolium.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017