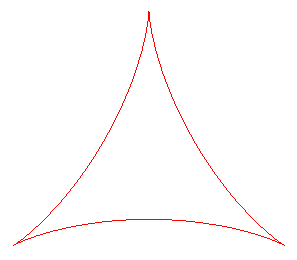
DELTOID
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DELTOID

| Curve studied by Euler in 1745 and Steiner in 1856.
Delta: Greek letter reminder of the shape of the curve. Other names: three-cusped hypocycloid, H3, Steiner hypocycloid, or tricuspid curve. |
 |
Complex parametrization: Cartesian parametrization: Cartesian equation: Rational circular quartic. Polar parametrization: Curvilinear abscissa: 1) 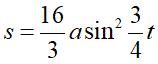 . .
Cartesian tangential angle: 1) Radius of curvature: 1) Intrinsic equation 1 (1st form): Intrinsic equation 2 (1st form)): Polar equation: Length: Area: |
The deltoid is the hypocycloid with three cusps (circle with radius a rolling inside a circle with radius 3a).
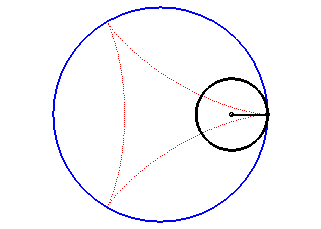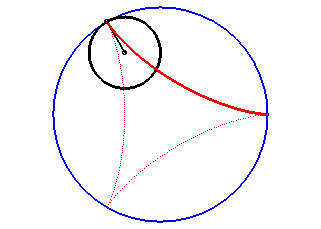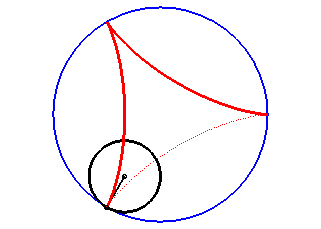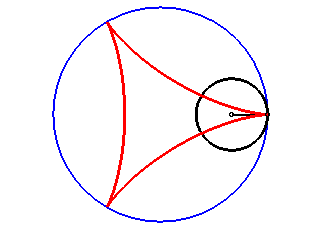
| According to the double generation of hypocycloids, a point on a circle with radius 2a rolling inside a circle with radius 3a describes an isometric deltoid, but in the opposite directions and one of its diameters also envelopes an isometric deltoid. | 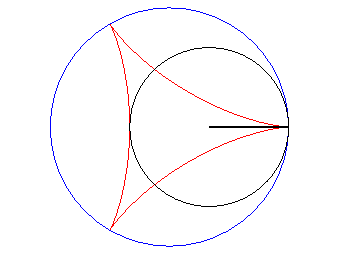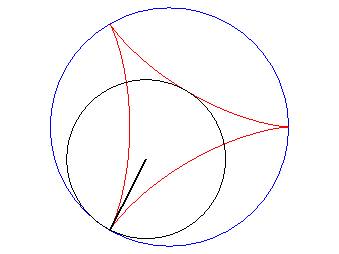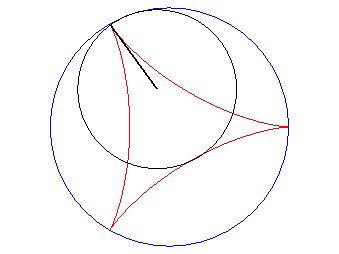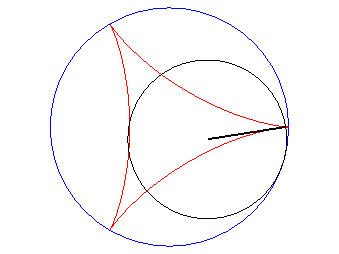 |
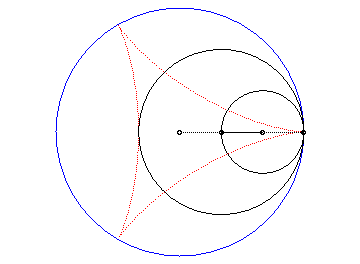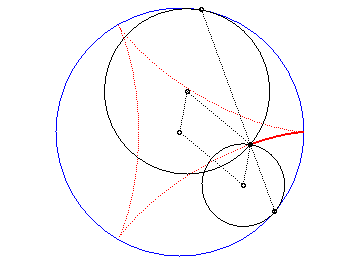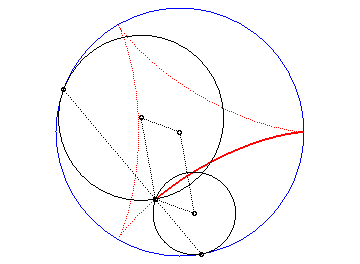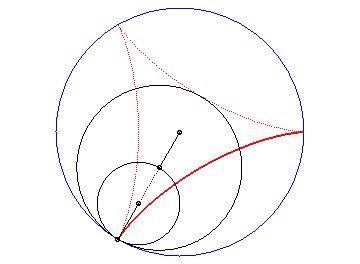
Slowed down animation of the double generation |
|
|
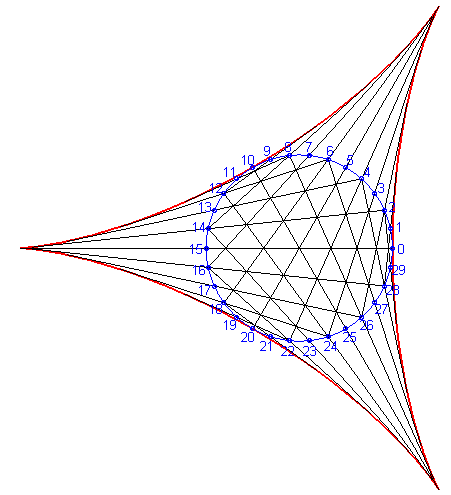
Above, the point n is linked to the point -2n modulo 30. |
 |
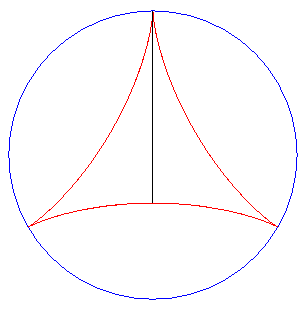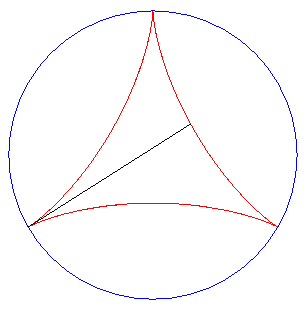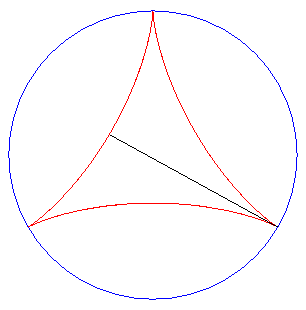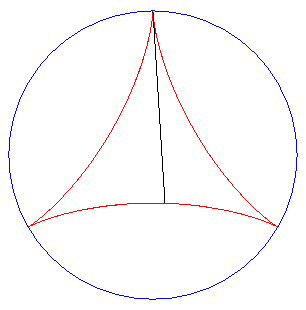
| But the most elegant tangential generation is the one described opposite: the two tracing points P and Q describe the deltoid, and the line (PQ) stays tangent to the same deltoid! |
|
| Furthermore, the fact that the length PQ remains
constant gives a (partial) answer to the problem
of Kakeya: how to turn around a needle (of length 1) in the plane in
such a way that it span an area as small as possible?
Here, the area spanned equals Remark: watch out! the needle slips on the deltoid during its movement! |
 |
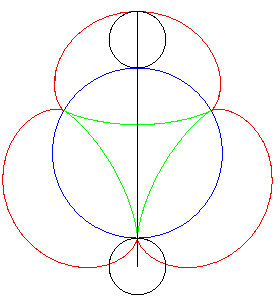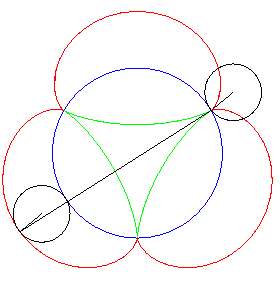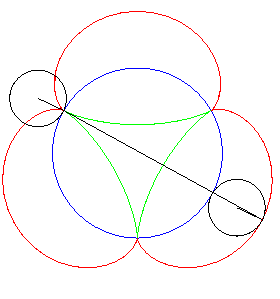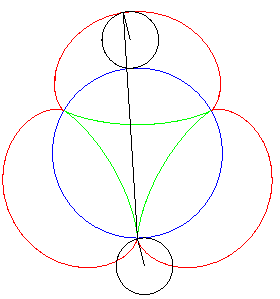
| Another mechanical construction of the tangential generation, dual to the previous one, stemming from the three-cusped epicycloid . |
 |
| The envelope of the Simson
lines (that pass by the projections on the three sides of a point on
the circumscribed circle) of any triangle is a deltoid centred on the nine-point
circle of the triangle, called the
Steiner hypocycloid of the triangle.
See details on Wikipedia. |
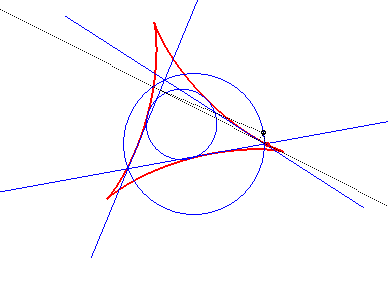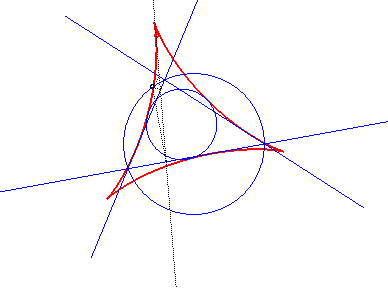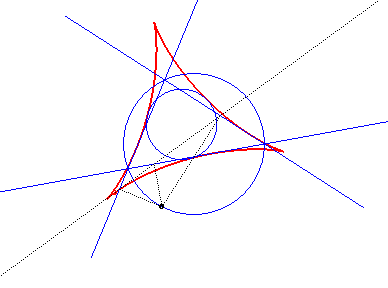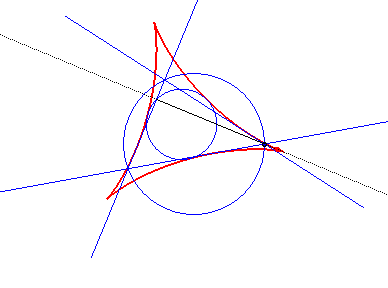 |
|
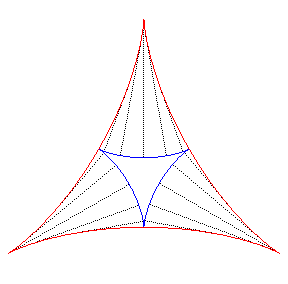
Like for any cycloidal curve, the evolute of the deltoid is a similar deltoid (with ratio 3): |
 |
|
Therefore, one of the involutes is a deltoid; the others are auto-parallel: |
 |
The pedals of the
deltoid are the folia, and the negative
pedal of an ellipse with respect to its principal summit gives a dilated
deltoid (see Talbot curve).
Its caustic by reflection
at infinity are the astroids.
Its orthoptic
is its inscribed circle.
Its radial is
a regular trifolium.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017