DUAL D'UN POLYCHORE
Dual of a polychoron, Dual eines Polychors
Si (P) est un polychore
(polytope de dimension 4), notons 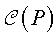 l'ensemble formé des ensembles des sommets de toutes les k-cellules
de (P) , pour k allant de –1 à 4 (la (–1)-cellule
étant par convention l'ensemble vide) ;
l'ensemble formé des ensembles des sommets de toutes les k-cellules
de (P) , pour k allant de –1 à 4 (la (–1)-cellule
étant par convention l'ensemble vide) ;
deux polychores (P) et (P*) sont alors
dits combinatoirement duaux s'il existe une dualité
de 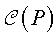 dans
dans 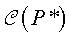 ,
c'est-à-dire une bijection envoyant les k-cellules de l'un
sur les (3 – k –1) cellules de l'autre qui renverse les inclusions
(autrement dit, si C1 est une cellule de C2, elle-même cellule de
(P) , C2* est une cellule de C1* (l'existence d'une bijection conservant
les types de cellules et leurs inclusions signifiant l'équivalence
combinatoire des polytopes).
,
c'est-à-dire une bijection envoyant les k-cellules de l'un
sur les (3 – k –1) cellules de l'autre qui renverse les inclusions
(autrement dit, si C1 est une cellule de C2, elle-même cellule de
(P) , C2* est une cellule de C1* (l'existence d'une bijection conservant
les types de cellules et leurs inclusions signifiant l'équivalence
combinatoire des polytopes).
Dans une dualité, les sommets de l'un des polychores
corespondent donc aux cellules de l'autre, et les arêtes aux faces
de l'autre.
Un dual d'un dual est un polychore équivalent
au polychore de départ.
| Une première méthode pour déterminer
un dual d'un polychore est de choisir un point dans chaque cellule (son
"centre"), et de relier par une arête deux points situés dans
des cellules contiguës ; les faces du dual sont alors celles qui sont
bordées par des arêtes joignant des "centres de cellules aboutissant
à la même arête du polychore de départ
; il faut pour cela que ces arêtes soient coplanaires et que donc
les centres choisis dans toutes les cellules aboutissant à une même
arête soient toujours coplanaires ; ceci est réalisé
si les arêtes du polychore de départ sont de degré
3, ou si le polychore est régulier (en choisissant dans chaque cellule
le centre de celle-ci). |
Une deuxième méthode, valable pour tout
polychore
convexe utilise la polarité par rapport à une hypersphère
:
Considérons une polarité
(ou dualité) par rapport à une sphère centrée
en un point intérieur au polychore (P) ; à tout sommet
du polychore de départ correspond par cette polarité un 3-espace
qui définira une cellule du polyèdre dual polaire (P*),
les sommets de cette cellule étant les points image par la dualité
des 3-espaces contenant les cellules qui aboutissent au sommet de départ.
| Les 3-espaces contenant les cellules du dual polaire
(P*) d'un polyèdre inscriptible (P) obtenu
par polarité par rapport à l'hypersphère circonscrite
sont les 3-espaces tangents à l'hypersphère passant
par les sommets de (P) ; inversement, les sommets du dual d'un polychore
circonscriptible sont les points de tangence avec la sphère inscrite. |
|
Les arêtes de (P) sont orthogonales aux faces
du dual polaire, et réciproquement.
© Robert FERRÉOL
2009