Anallagmatic curve

ANALLAGMATIC CURVE

Notion studied by Moutard in 1864.
Anallagmatic literally means: without change (from the Greek allagma "change").

General polar equation: with .

A curve is said to be anallagmatic if it is globally invariant by inversion.

Any anallagmatic curve can be generated as a cyclic curve, i.e. as the envelope of circles, orthogonal to the circle of inversion (in the case of a positive power), the centres of which describe one of the deferential curves of the curve (in the plural form, because we can indeed have several generations of this type there):

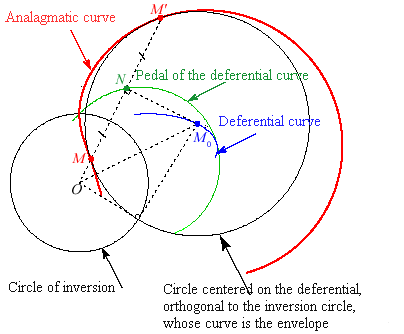
In the algebraic case, it is always circular.

Examples of anallagmatic curves:
    - the straight line (with respect to one of its points)
    - the circle
    - the strophoids (the circle of inversion is centered at the focus (on the loop) and pass by the double point, the deferential curve is a parabola passing by the double point).
    - More generally all circular cubics (the pole of inversion is the point of the cubic where the tangent is parallel to the real asymptote).
    - the Pascal's snails (with respect to the point of abscissa on Ox).
    - the Casinian and Cartesian ovals.
    - more generally the bicircular quartics and circular ones with double point.
    - anallagmatic spirals.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra