Simple folium

SIMPLE FOLIUM

Curve studied by Kepler in 1609 and Viviani in 1647.
Other names: ovoid, or Kepler egg.

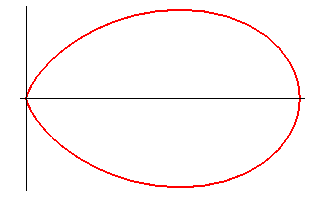
Despite appearances to the contrary, there is a (vertical) tangent at O;
On the other hand, the radius of curvature is zero whereas it is not at the other end, cf the egg and its evolute below.

Polar equation:

(Clairaut's curve).
Cartesian equation:

.
Rational Cartesian parametrization:

.
Rational circular quartic.
Radius of curvature:

.
Length:

.
Area:

.
Volume of the solid of revolution (that can be called Kepler ovoid) obtained by rotating the folium around its axis:

.
Lateral area:

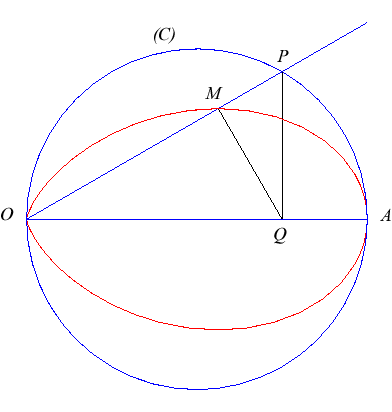
Given a circle (C) with diameter [O A], and a variable point P describing (C), the simple folium is the locus of the projection M on (D) of the projection Q on (OA) of P.
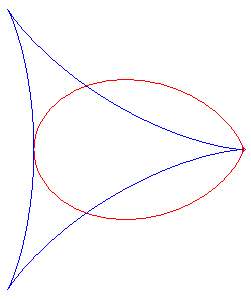
The simple folium is the pedal of the deltoid with respect to one of its cuspidal points; it is therefore a special case of bifolium and of right folium, the other being the regular bifolium.
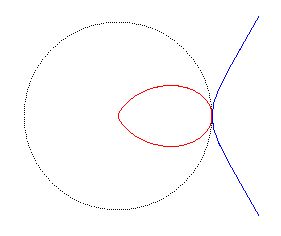
It is also the inverse of the duplicatrix cubic with respect to its isolated point.

Compare to the double egg ( instead of ) and see other eggs at ovoid.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra