FREETH'S NEPHROID
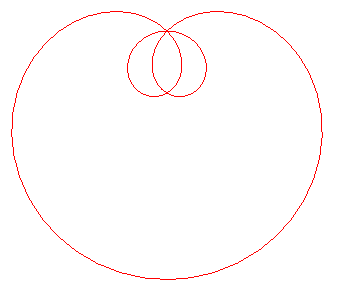
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
FREETH'S NEPHROID

| Curve studied by Freeth in 1879.
T. J. Freeth (1819 - 1904): British mathematician. Loria p. 329. |
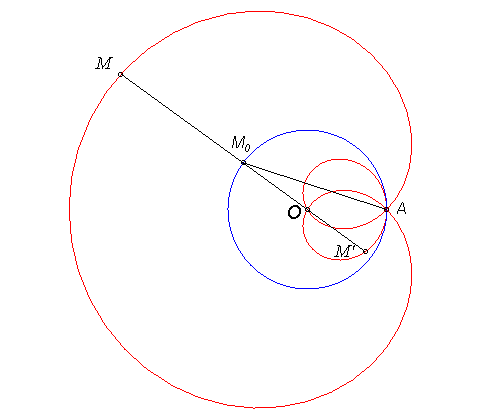
| Freeth's nephroid is the strophoid
of a circle with respect to two points O and A, A
being on the circle and O the centre of the circle: when a point
M0
describes the circle, the curve is the locus of the points M of
the line (AM0) such that M0M
= M0A.
|
 |
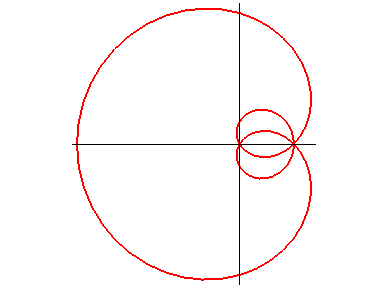 |
In the frame with centre O such that A(a,0):
Polar equation: Cartesian equation: Rational sextic (double point at O, triple at A). |
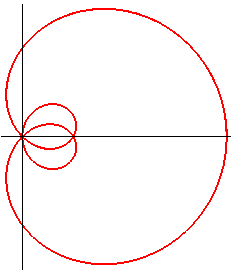 |
In the frame centred on A such that O(a,0):
Pedal equation: Complex parametrization: Area of the domain delimited by the external part: |
The first equation shows that Freeth's nephroid is a conchoid
of the Dürer folium.
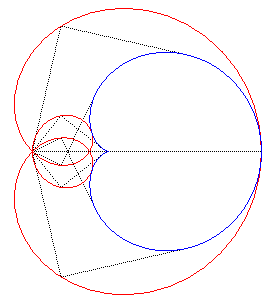
| But Freeth's nephroid is also the pedal
of the cardioid: |
 |
| The complex parametrization above shows that Freeth's nephroid is a tritrochoid. |
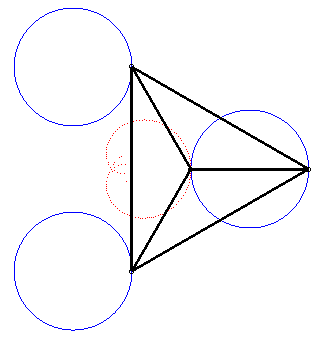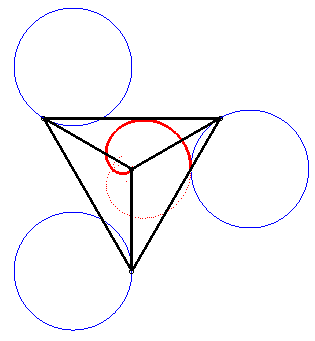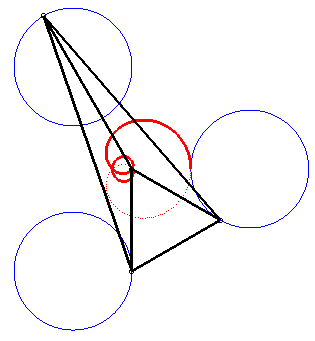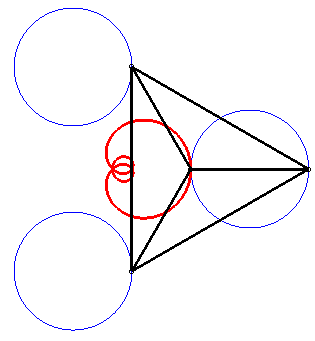 |
For ,
;
Freeth's nephroid enables to construct the regular heptagon.
GENERALIZATION
| The Freeth's nephroid is the case n = 4 of the
family of curves of complex parameterization: The case n = 3 gives the limaçon trisectrix and when n tends to infinity, the limit curve is the cochleoid: |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2020