| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ANTICAUSTIQUE
Anticaustic,
Gegenbrennlinie
| Notion étudiée par Quételet
en 1825 et Mannheim
en 1861.
Autre nom : caustique secondaire (nom donné par Quételet). Attention, le nom d'anticaustique est aussi parfois donné à la notion désignée dans ce site par "caustique inverse". |
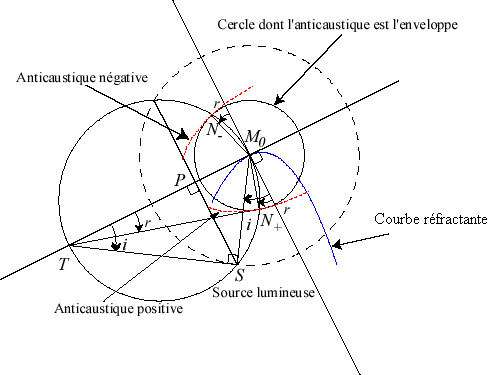
L’anticaustique (par réfraction) d'une courbe 
(la courbe réfractante), par rapport à un point S,
et associée à une constante n > 0 est l'enveloppe
d'un cercle (C) centré en M0
sur et
de rayon 
; autrement dit, le rayon reste dans un rapport constant avec la distance
de M0 à
la source lumineuse.
Son nom provient de ce que cette courbe sert à
déterminer la caustique par réfraction
complète de (G0)
pour
S et n (n est le rapport 
des indices de réfraction de l'autre côté de S
et du côté de S, donc aussi le rapport des vitesses
de la lumière du côté de S et de l'autre côté)
; la caustique est en effet la développée de l'anticaustique.
| Les points caractéristiques du cercle (C),
M+
du côté de S et M-
de l'autre, sont les points d'intersection de (C) avec le cercle
de diamètre [M0T],
où T est le point d'intersection de la tangente (T0)
en M0 à (G0)
avec la normale en S au rayon incident (SM0).
Ici,  où
i
est l'angle avec la normale du rayon incident, r celui du rayon
réfracté ; d'où  .
M+ décrit l'anticaustique positive, dont la développée est la caustique par réfraction associée à la constante +n, et M- décrit l'anticaustique négative, dont la développée est la caustique par réfraction associée à la constante -n. |
 |
Lorsque n = 1, l'anticaustique est l'orthotomique,
et la caustique est alors la caustique par réflexion.
Les anticaustiques de droite sont les coniques.
Plus précisément, si S' est le symétrique
de S par rapport à une droite (D), l'anticaustique
de (D) par rapport à S pour la constante n
est
- l'ellipse de foyers S et
S'
et d'excentricité n : 
si n < 1.
 |
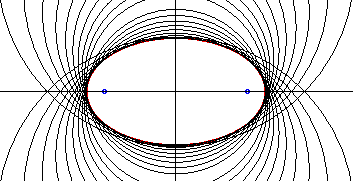L'ellipse est l'enveloppe des cercles centrés
sur son axe non focal et dont le rayon vaut le rapport de la distance de
son centre au foyer avec l'excentricité de l'ellipse.
L'anticaustique positive est la partie située du côté de S par rapport à (D), et l'anticaustique négative, l'autre partie. |
- l'hyperbole de foyers S et
S'
et d'excentricité n : 
si n > 1.
 |
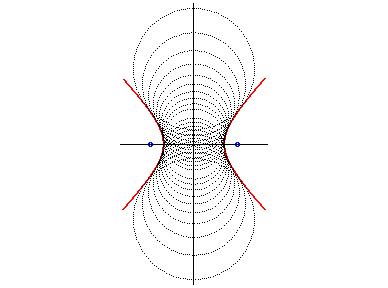L'hyperbole est l'enveloppe des cercles centrés
sur son axe non focal et dont le rayon vaut le rapport de la distance de
son centre au foyer avec l'excentricité de l'hyperbole.
L'anticaustique positive est la branche située du côté de S, et l'anticaustique négative, l'autre branche. |
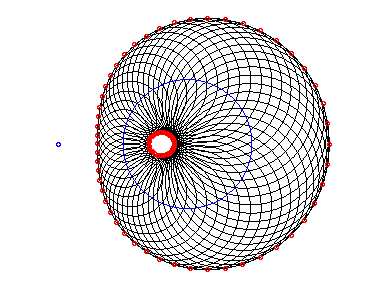
Les anticaustiques de cercle sont les ovales de Descartes complets (comprenant les limaçons de Pascal, obtenus lorsque la source lumineuse est sur le cercle).
Plus précisément, si S' est le conjugué
de S par rapport à un cercle (C) de centre O
et de rayon R, l'anticaustique de (C) par rapport à
S
pour la constante n est l'ovale de Descartes complet : 
, où 
.
Les anticaustiques possèdent deux belles propriétés
de réciprocité, constituant les théorèmes de
Mannheim :
1) l'inverse de l'anticaustique est l'anticaustique de l'inverse.
2) l'anticaustique de l'anticaustique (avec le même indice n
et par rapport au même point lumineux F) est une courbe semblable
à la courbe de départ (centre F et rapport 1-1/n2).
Exemple d'application : la caustique par réfraction complète
d'un ovale de Descartes complet par rapport à un foyer étant
un autre foyer, l'anticaustique est un cercle. Les anticaustiques de cercles
sont donc les ovales de Descartes complets.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2000