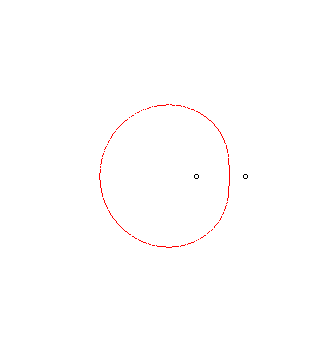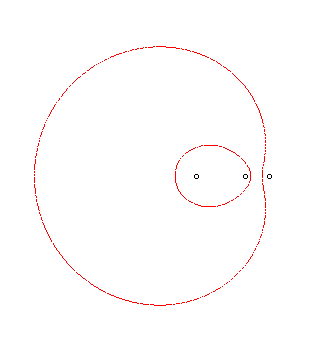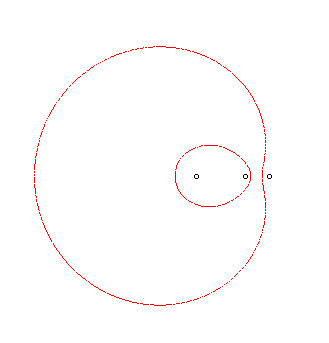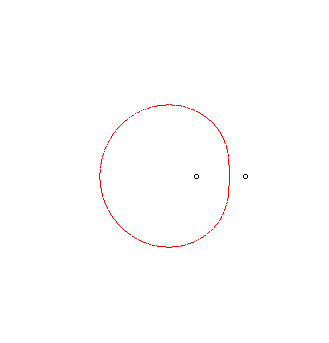
Les ovales de Descartes sont les lieux des points dont la moyenne pondérée des distances à deux points fixes est constante.

Plus précisément, ce sont des lieux de points M dont les distances MF et MF' à F et F' sont liées par une relation du type : , avec  (les cas limites de l'ellipse et de l'hyperbole sont donc exclus).

REM : La courbe est non vide ssi , et .
 

Ci-contre est présentée une construction mécanique de l'ovale de Descartes, dans le cas où v/u = 2, construction qui se généralise (théoriquement !), à condition d'enrouler suffisamment le fil autour des poulies, aux cas où v/u est un rationnel positif. A droite illustration dûe à Descartes lui-même.

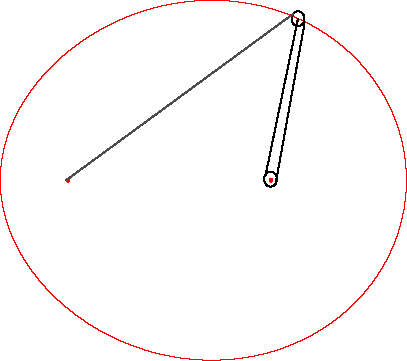Autre construction mécanique, due à J. Hammond (1878). Les deux poulies sont solidaires, leur axe commun a une position arbitraire dans le plan de la figure, seul le rapport de leur rayon égal à v/u importe. Les foyers choisis, on enroule deux fils, en sens inverse, sur les poulies. La pointe du crayon, fixe par rapport au fil, est fixée à l'autre extrémité de chacun des deux fils. Illustrations dues à Jean lochet.

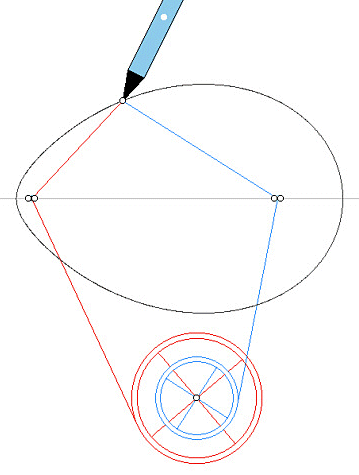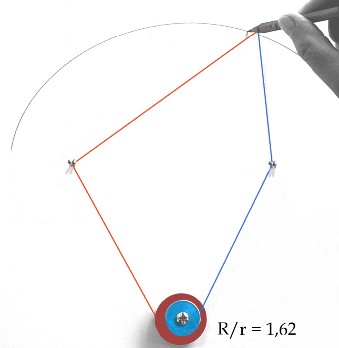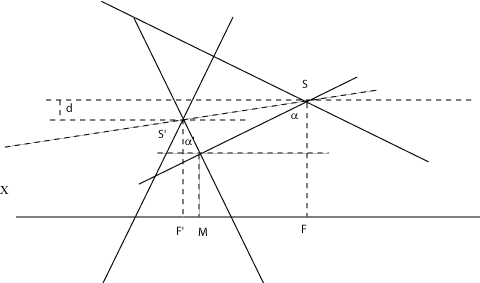
Une construction dans l'espace : les ovales de Descartes sont les projections des intersections de deux cônes de révolution d’axes parallèles sur un plan perpendiculaire à ces axes (théorème de Quételet). Plus précisément, le cône  et le cône  ont une intersection qui se projette en les ovales de Descartes :. A droite, démonstration géométrique, pour des cônes de sommets S et S' et de demi-angle au sommet a et a' : .

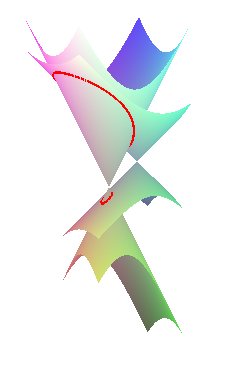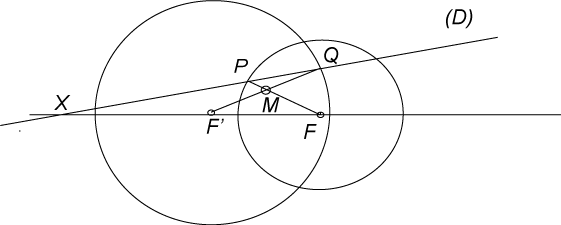
Cette construction est à l'origine d'une construction plane, dûe à Chasles, dont on peut oublier l'origine 3D ; coupons les 2 cônes par un plan (P0) perpendiculaire aux axes, ce qui donne deux cercles (C) et (C') de centres F et F' ; la droite joignant les sommets S et S' des deux cônes coupe (P0) en X, aligné avec F et F' ; tout plan (P) passant par F et F' coupe (P0) en une droite (D) passant par X ; ce plan (P) coupe les deux cônes suivant deux génératrices, lesquelles se croisent en un point de l'intersection des deux cônes ; en projection, la droite joignant F à un point d'intersection de (C) avec (D) et la droite joignant F' à un point d'intersection de (C') avec (D) se coupent en un point M de l'ovale de Descartes projection de l'intersection des deux cônes (et comme il y a deux points d'intersection avec chaque cercle, il y a 4 points M ainsi construits). Quand la droite (D) pivote autour de X, les 4 points M décrivent chacun un demi ovale de Descartes. On obtient ainsi deux ovales de Descartes conjugués (voir la définition plus loin). Origine : [Zwikker, p. 124]	Démonstration sans faire intervenir l'espace : le théorème de Ménélaüs dans le triangle MFF' pour la transversale (D) donne , d'où
Etant donnés deux cercles (C) et (C') de centres F et F' de rayons R et R' supérieurs à FF', on obtient l'ovale de Descartes  en faisant passer deux droites variables parallèles (D) et (D') par F et F', la première coupant (C') en N et la deuxième (C) en N' , du même côté de (FF') ; le point d'intersection M de (FN') et de (F'N) décrit l'ovale de Descartes. Démonstration : par Thalès MF.MF' = MN. MN'=(R'-MF')(R-MF) d'où R' MF +R MF' = RR'. On obtient ainsi tous les ovales non vides , avec u,v,c > 0 (). Cette construction est une généralisation de la construction de l'ellipse par parallélogramme croisé (cas R = R').
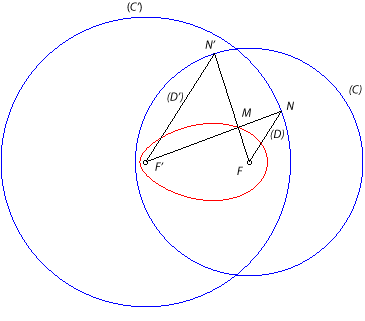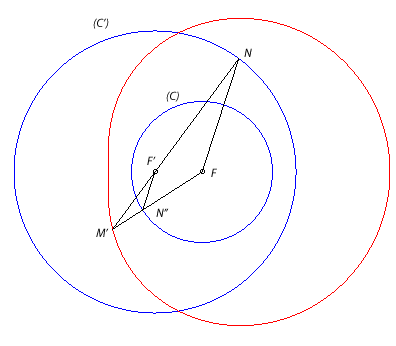
Si l'on reprend la construction précédente en prenant les points d'intersection N de (D) avec (C') et N'' de (D') avec (C) de part et d'autre de (FF'), le point d'intersection M' de (FN") et de (F'N) décrit cette fois l'ovale de Descartes conjugué du précédent d'équation (cas R' > R). Démonstration : par Thalès M'F.M'F' = M'N. M'N"=(R'+M'F')(-R+M'F) d'où R' M'F -R M'F' = RR'.

 

En posant R = 2a, R'=2b, F=(0,c), F'=(– c,0), la construction ci-dessus fournit les paramétrisations suivantes  des ovales  et , avec ,  : et . Rem : le cas R et R' > FF' étudié ici correspond à celui où les deux foyers sont internes à l'ovale ; les autres cas donnent le troisième foyer (voir plus loin).

 

La tangente en M à l’ovale est orthogonale au vecteur .  Si donc  et  sont les angles que font avec la normale en M les segments MF et MF', on a la relation . On en déduit la propriété qui a motivé l’étude de ces courbes par Descartes : si la partie externe d’un ovale de Descartes contenant F est d’indice de réfraction n1  et l’interne contenant F' d’indice n2 avec , les rayons lumineux issus de F et réfractés par l’ovale convergent vers F' (à condition que [MF] soit entièrement à l’extérieur et [MF’] à l’intérieur) ; de là vient le nom de courbe aplanétique. On retrouve aussi cette propriété par le fait que la longueur du chemin optique est constante.

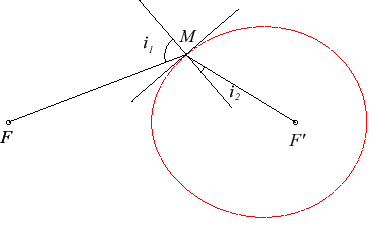
Figure avec l'ovale MF+3MF'=2FF'. On a donc ici .

Plus généralement, la caustique par réfraction de l'ovale pour le point lumineux F et le rapport u/v est le foyer F' : les ovales de Descartes sont les courbes dont une caustique par réfraction est réduite à un point.

L'ovale de Descartes complet associé est l'ensemble d'équation bifocale : .
Parmi les 4 courbes obtenues par ces doubles signes, seules deux sont non vides, et ces deux ovales sont dits conjugués.
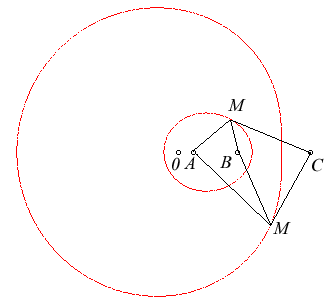
On démontre que l'ovale de Descartes possède un troisième foyer, aligné avec les deux premiers, tel que les équations bifocales dans les deux nouveaux couples de foyersles obtenus sont encore du même type.
Les relations entre ces foyers et les équations sont données ci-dessous. Nous avons renommé les foyers " A, B, C ", par parallélisme avec  ; ce sont ces notations que nous utiliserons dorénavant.
 

Si  sont les trois foyers de l'ovale complet, avec  : Équations bifocales équivalentes de l'ovale extérieur : . Équations bifocales équivalentes de l'ovale intérieur : . Pour l'ovale , le point O et le foyer F'' sont définis par :
Animation du cas  ; le foyer B se déplace de A vers C ; les deux cas limites sont des limaçons de Pascal.

Équation cartésienne de l'ovale complet dans le repère  : , où  sont les fonctions symétriques élémentaires de . Abscisses des 4 sommets :  (ovale extérieur) et  (ovale intérieur). Équation polaire de l'ovale complet dans le repère  :  où, , . Équations similaires obtenues par permutation de  dans les repères  et . Équation cartésienne dans  : . Quartique bicirculaire, elliptique dans le cas d'un ovale véritable.

L'équation polaire  montre que les ovales de Descartes complets sont anallagmatiques : ce sont des cycliques de déférente un cercle, autrement dit des cartésiennes. Plus précisément, ce sont les cartésiennes dont les trois foyers réels sont alignés.
Pour le foyer A, le cercle déférent est le cercle de centre O et de rayon  où , le cercle directeur, celui de centre A et de rayon  (pour les deux autres foyers, les définitions sont obtenues par permutation).

Lorsque les trois foyers sont distincts, l'ovale est dit véritable. Il possède alors trois définitions cycliques distinctes : Vue des 3 générations cycliques d'un même ovale de Descartes complet ; les cercles noirs sont centrés sur le cercle déférent (en bleu), lui-même centré en O, et sont orthogonaux (ou pseudo-orthogonaux pour celui de droite) au cercle directeur (en vert), centré en l'un des foyers A, B ou C ; on a pris ici, a = 1, b = 2, g = 3.

Les six cercles directeurs et déférents.

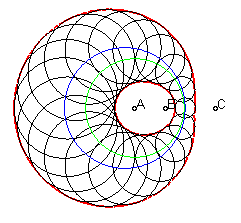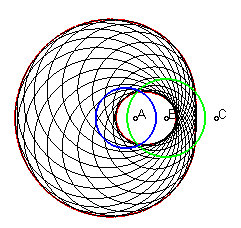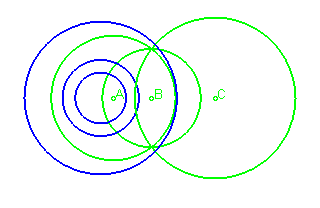
Lorsque les 3 foyers sont confondus (), l'ovale est une cardioïde (mais il perd ses définitions bifocales).
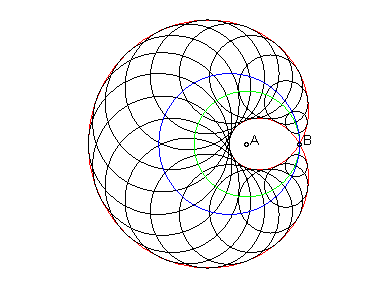
Lorsque seuls deux foyers sont confondus sur les 3, on obtient un limaçon de Pascal :
     - lorsque A = B, on obtient le limaçon elliptique :  (dans ), d'équation bifocale : , qui possède deux générations cycliques, dont une seule est à puissance nulle.
 

génération à puissance nulle (cercles passant par A et centrés sur le déférent)

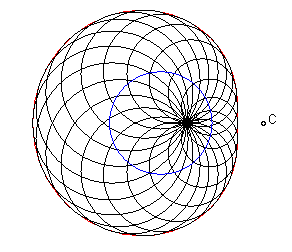 - lorsque B = C, on obtient le limaçon hyperbolique : (dans ), d'équation bifocale :  pour la boucle extérieure, et  pour la boucle intérieure, qui possède deux générations cycliques, dont une seule est à puissance nulle.
 

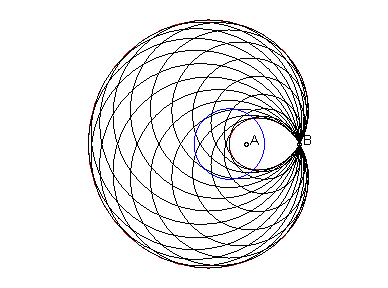
génération à puissance nulle (cercles passant par B et centrés sur le déférent)

Les ovales de Descartes complets peuvent aussi être définis comme les anticaustiques de cercle (les limaçons de Pascal étant obtenus lorsque la source lumineuse est sur le cercle). Les développées d'ovales de Descartes complets sont donc les caustiques par réfraction de cercle.

Voici des lieux géométriques qui donnent des ovales de Descartes :

1) Lieu d'un point dont les "distances algébriques" à deux cercles fixes de rayons distincts sont dans un rapport constant différent de ± 1 (auquel cas on obtiendrait les coniques bifocales) ; la "distance algébrique" d'un point à un cercle est sa distance au centre moins le rayon. Les ovales de Descartes sont donc les lignes de partage de deux cercles.
 

Lignes de partage de deux cercles, définies par . En vert pour k > 1, en bleu pour 0 < k < 1 , en rouge pour k = 1 (branche d'hyperbole, médiatrice des deux cercles).

 

2) Étant donnés 3 points alignés F, G, H, lieu du sommet M d'un triangle LMN dont les côtés (NM), (ML), (LN) contiennent respectivement F,G,H, ([ML] et [MN] ayant des longueurs fixées (appliquer le théorème de Ménélaüs dans le triangle MFG).

On retrouve aussi les ovales de Descartes dans le système Bélidor de pont-levis.

Encore une propriété de ces courbes très riches : Les images des droites parallèles aux axes par une fonction elliptique P de Weierstrass de périodes w₁ réelle et w₂ imaginaire pure sont des ovales de Descartes.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2023