La courbe en pointillé est le folium de Dürer, dont la trisectrice de Delanges est l'inverse.

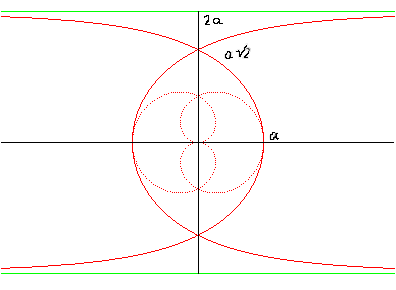Équation polaire : . Paramétrisation cartésienne :  (t = q / 2). Équation cartésienne : . Quartique circulaire rationnelle.

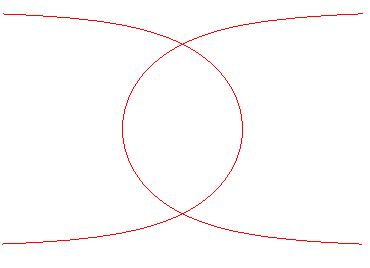
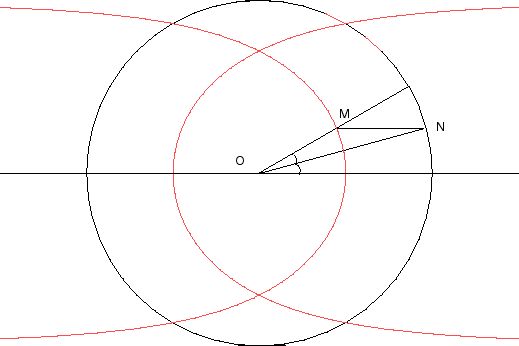
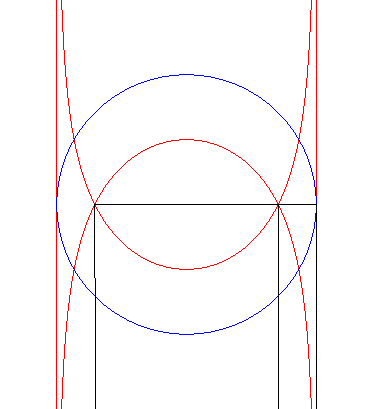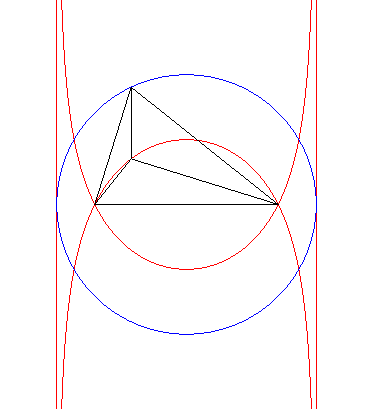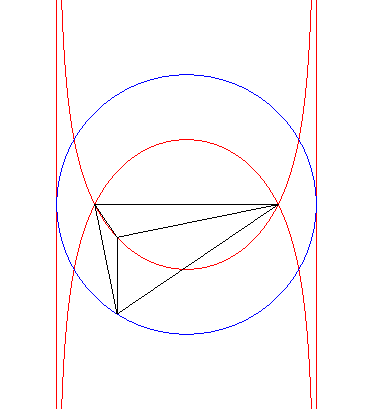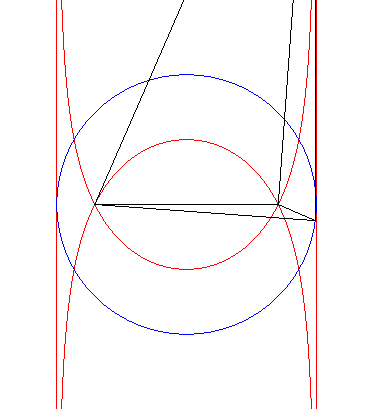
Etant donnés un cercle (C) (ici, le cercle de centre O et de rayon 2a) et une droite (D0) passant par le centre du cercle (ici Ox), la trisectrice de Delanges est le lieu d'un point M d'une droite variable (D) passant par O tel que la parallèle à (D) passant par M coupe (C) en N de sorte que (ON) soit une bissectrice de (D0) et (D).
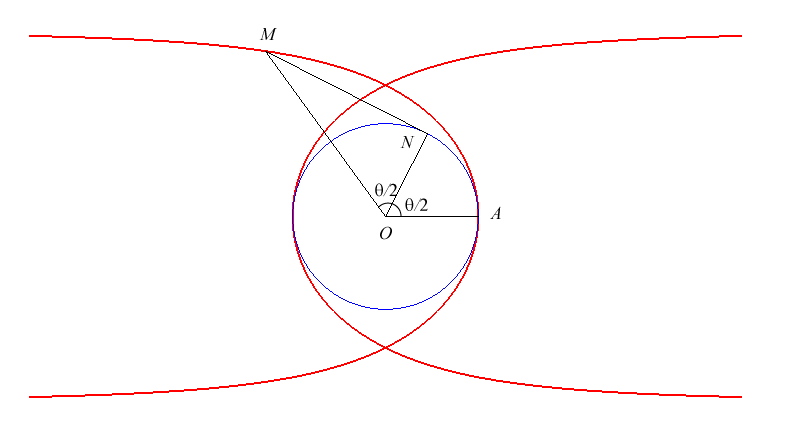
Construction équivalente à la précédente : le cercle est de rayon a, A en est un point fixe, N un point variable. La symétrique de la droite (OA) par rapport à (ON) coupe la tangente au cercle en N au point  M.
La trisectrice de Delanges est le lieu de l'orthocentre d'un triangle ayant un côté fixe dont le sommet opposé à ce côté décrit un cercle centré au milieu du côté et de rayon, la longueur du côté multipliée par . Voir une construction similaire pour le bicorne, la strophoïde droite, et le kappa.

La trisectrice de Delanges est un cas particulier d'épi.
 

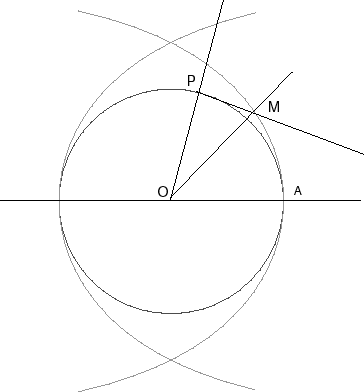
La construction ci-contre montre la propriété de trisection : l'angle MOP est le tiers de AOP.

Sa courbe inverse par rapport à O est le folium de Dürer, qui est donc aussi une trisectrice.

De plus, la même construction montre que la courbe d'équation  est une (n + 1)-sectrice, que l'on peut nommer "sectrice de Delanges".
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2024