ÉPITROCHOÏDE
Epitrochoid,
Epitrochoide
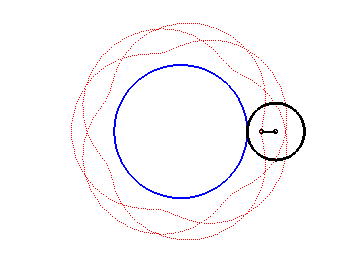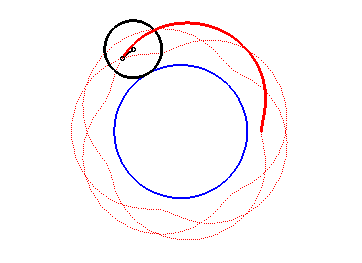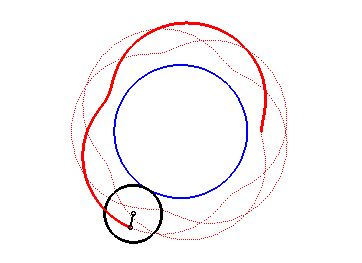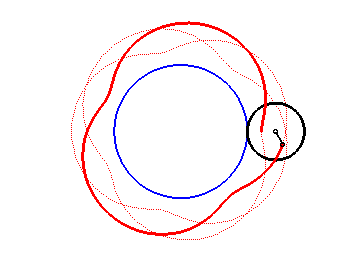
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ÉPITROCHOÏDE
Epitrochoid,
Epitrochoide


| Du grec epi "sur" et trokhos "roue".
Autre nom : épicycloïde allongée ou racourcie. Pour tracer des épitrochoïdes : aesculier.fr/fichiersMaple/cycloide/epihypocycloides.html |
| Paramétrisation complexe : Paramétrisation cartésienne : Paramétrisation polaire : Aire englobée par la courbe dans le cas |
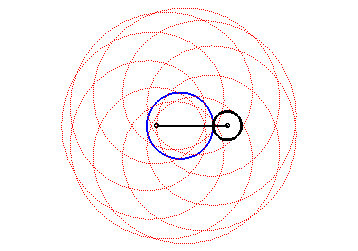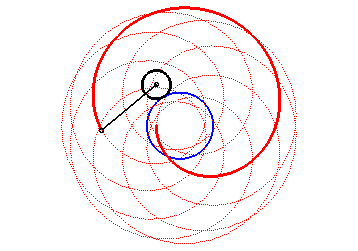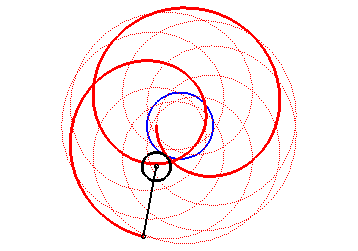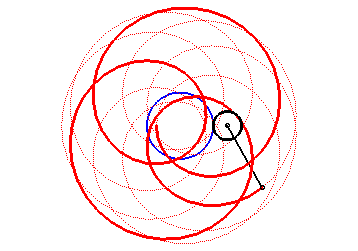
| Les épitrochoïdes sont les courbes décrites par un point lié à un cercle (C) roulant sans glisser sur un cercle de base (C0), les disques ouverts de frontières (C) et (C0) étant disjoints ; ce sont donc les courbes que l'on obtient avec un spirographe avec disque externe. |  |
Autrement dit, ce sont aussi les roulettes d'un mouvement plan sur plan dont la base est un cercle et la roulante un cercle extérieur au premier.
Pour d = b, soit k = 1, on obtient
les épicycloïdes.
Pour d = a + b, on obtient les rosaces
.
Pour k < 1, la courbe s'appelle aussi épicycloïde
raccourcie.
Pour k > 1, la courbe s'appelle aussi épicycloïde
allongée.
| Toute épitrochoïde est aussi une péritrochoïde
(propriété dite "de double génération") : cercle
fixe de rayon |
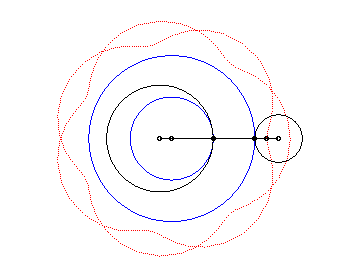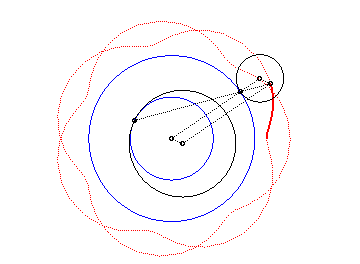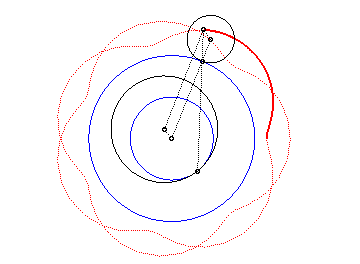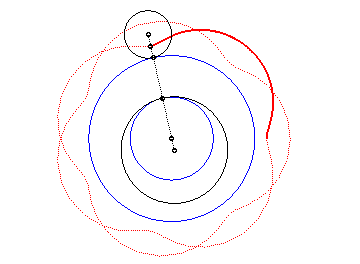 |
Voici les différentes formes en fonction des valeurs
de k.
| Il est remarquable que pour D'après cet article, c'est le cas de la trajectoire de la lune par rapport au soleil, pour laquelle Notons que pour la trochoïde rectiligne, il y a toujours des changements de concavité. |
|
| Le cas limite est |
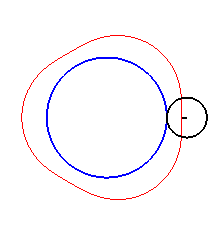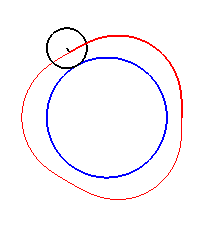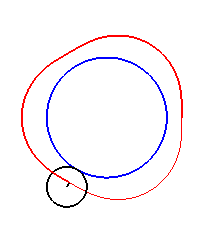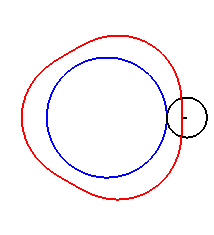 |
| Pour |
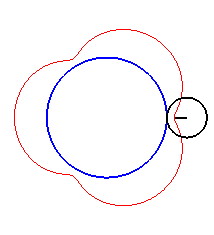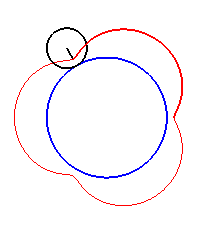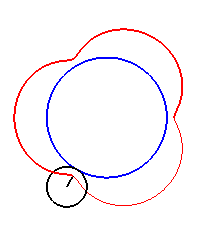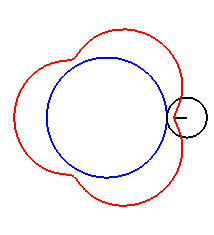 |
| Pour k = 1, on obtient l'épicycloïde, avec des points de rebroussements. |
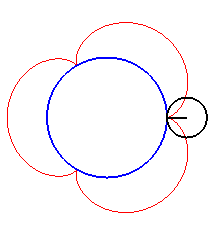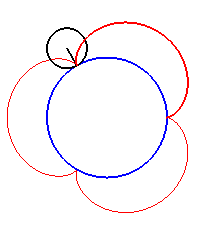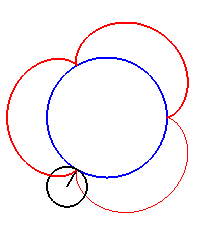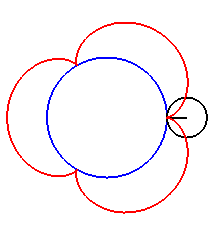 |
| Pour |
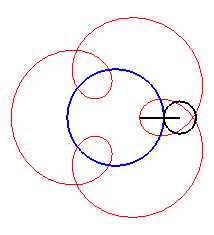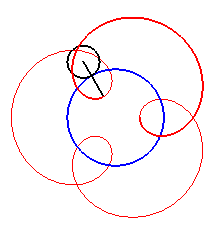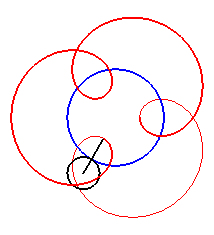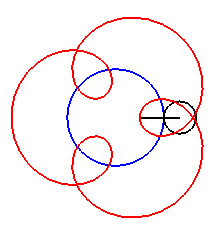 |
| Pour k = q + 1 (soit d = a
+ b)), on obtient une rosace
d'indice n < 1 , d'équation polaire |
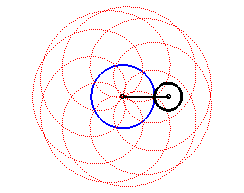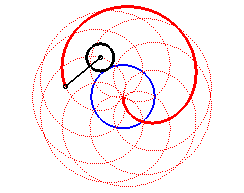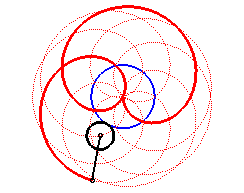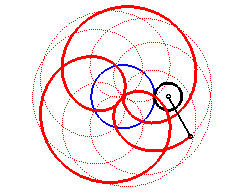 |
| Cas k > q – 1. |
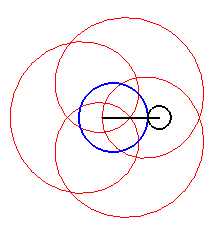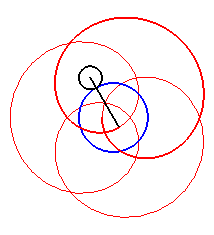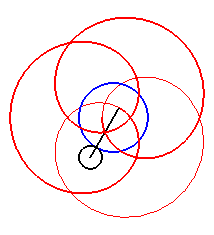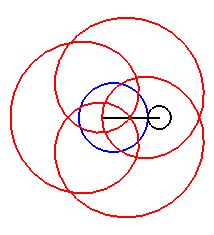 |
| On peut aussi définir les épitrochoïdes
comme les trajectoires d’un mouvement qui est composé de deux mouvements
circulaires de même sens et de vitesses angulaires distinctes, de
paramétrisation complexe : |
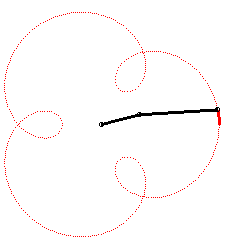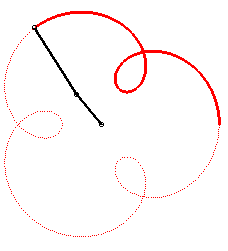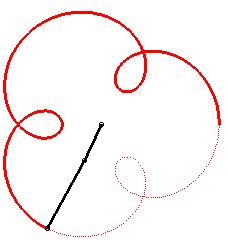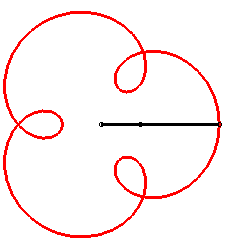
Le premier bras a une vitesse angulaire (par rapport au plan fixe) quadruple de celle du deuxième : on obtient une épitrochoïde de paramètre q = 4 - 1 = 3. |
| L'écriture |
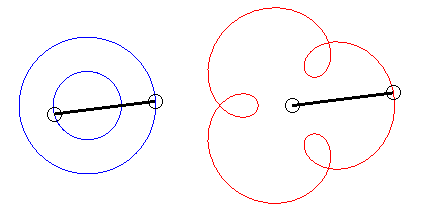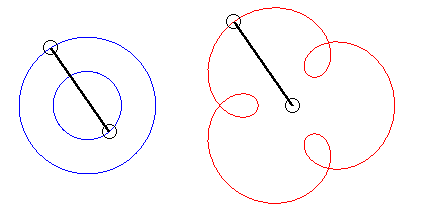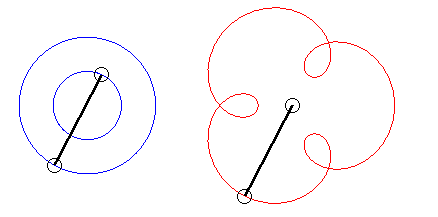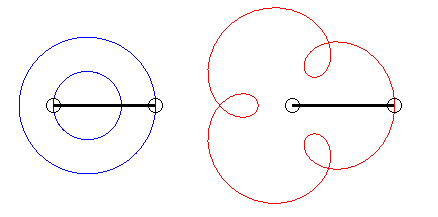 |
| En approximant les mouvements des planètes autour
du soleil à des mouvements circulaires uniformes et coplanaires,
on peut donc considérer que les trajectoires apparentes des planètes
les unes par rapport aux autres sont des épitrochoïdes. Ces
trajectoires étaient appelées des épicycles
(voir aussi cette
animation).
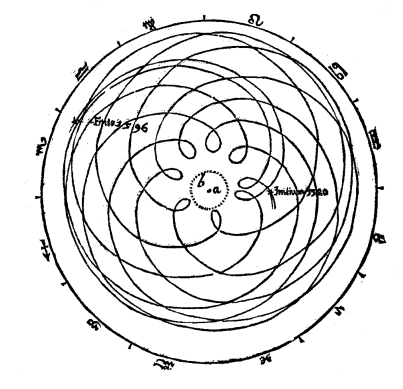
Ci-contre, esquisse réalisée par Kepler dans l'Astronomia nova, représentant l'évolution des lacets de l'orbite de Mars depuis la terre. |
 |
Forme des courbes dans les différents cas :
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
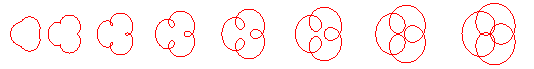 |
|
|
|
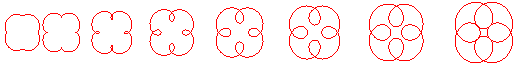 |
|
|
|
 |
|
|
|
 |
|
|
|
 |
Les épitrochoïdes sont aussi des projections planes des courbes de Caparéda, ou courbes des satellites, ainsi que des courbes de précession constante.
Les épitrochoides réunies avec les hypotrochoïdes constituent les trochoïdes à centre (voir aussi une généralisation sur le lien précédent).
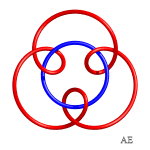
Voici diverses épitrochoïdes passées en 3D et nouées :
 |
 |
 |
 |
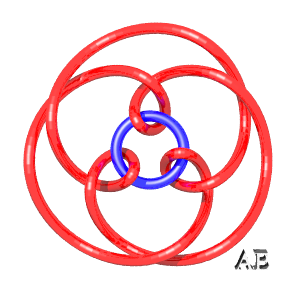
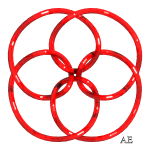
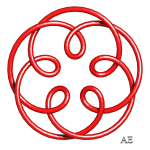
| q = 3, entrelacs 9.2.24 | q = 3, noeud 9.1.40 | q = 3/2, entrelacs à 12 croisements | q = 4, voir cette page |
 |
 |
 |
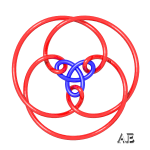 |
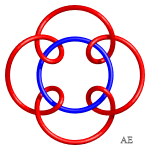
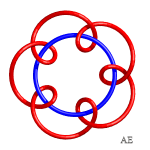
| q = 4, noeud à 12 croisements | q = 5, entrelacs à 15 croisements | q = 5/2, noeud 5.1.1 | q = 3/2 et q =3 entrelacées, entrelacs à 15 croisements |
| Courroie d'engrenage, mise en forme d'épitrochoïde par Lévi Capareda pendant un cours de sciences industrielles... | 
|
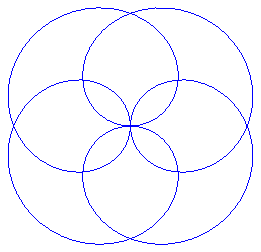 |

p = 4, k = 4 |
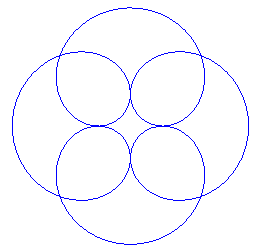 |
| Idem avec q = 2 (folium de Dürer) | 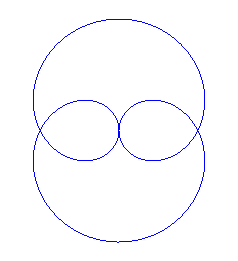 |
 |
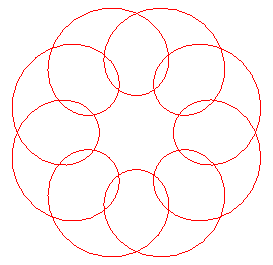
| Ce motif d'une tapisserie arabe a la même structure que l'épitrochoïde avec p = 8, k = 5 (tourner d'un seizième de tour). |
 |
 |
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2017