Quartique rationnelle (point singulier en O) située dans la bande
Equation polaire :
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
KIÉROÏDE
Kieroid
| Courbe étudiée par Kiernan en 1945, d'où
le nom (voir
Yates).
P. J. Kiernan : ?? |
| Equation cartésienne : Quartique rationnelle (point singulier en O) située dans la bande Equation polaire : |
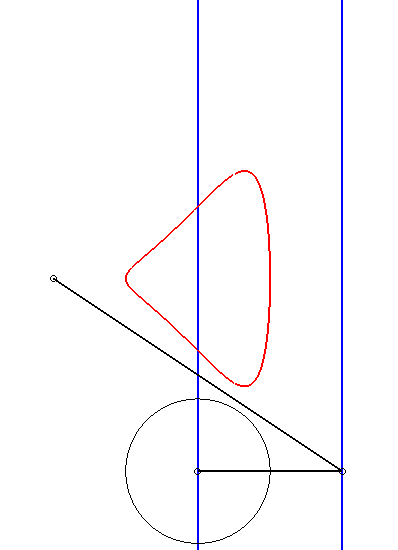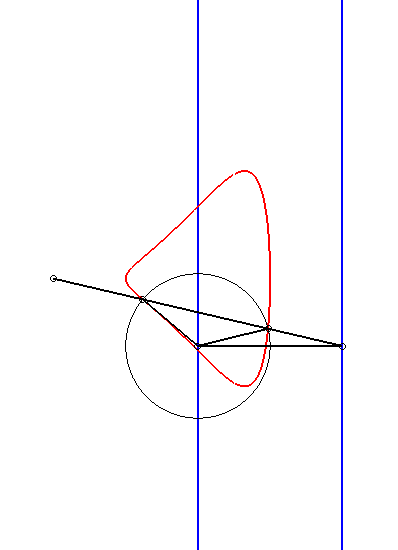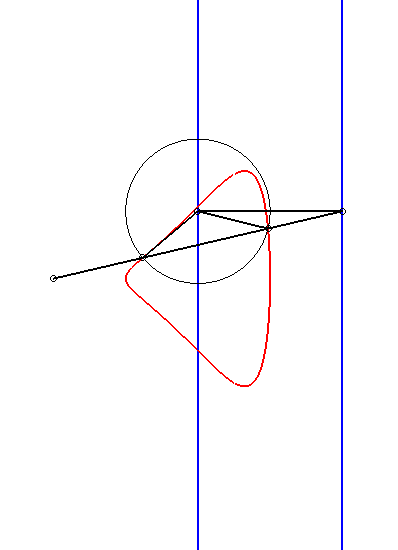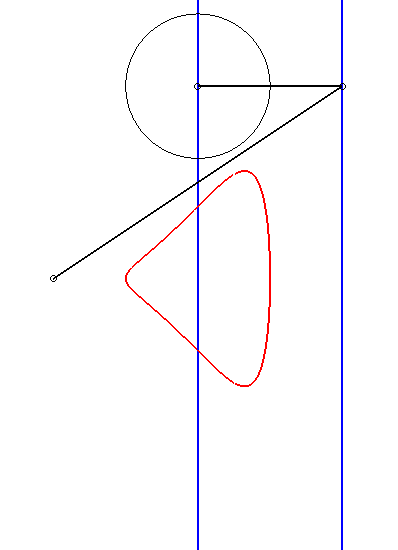
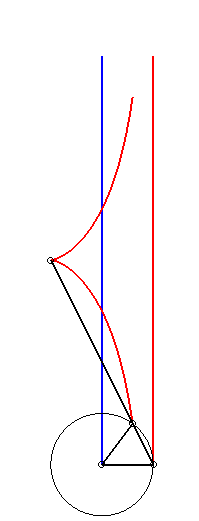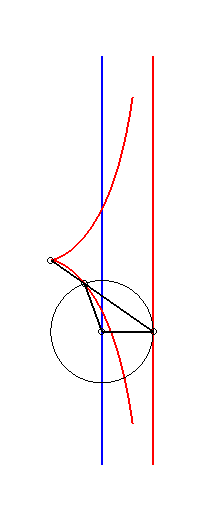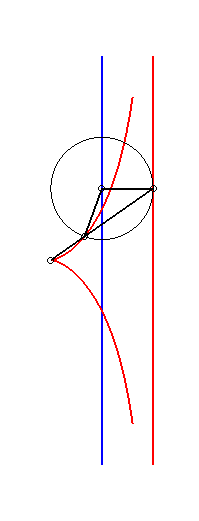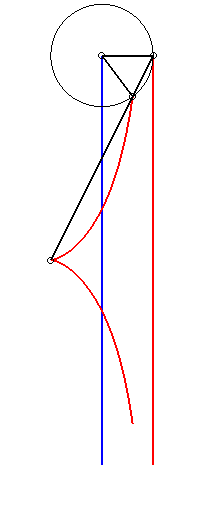
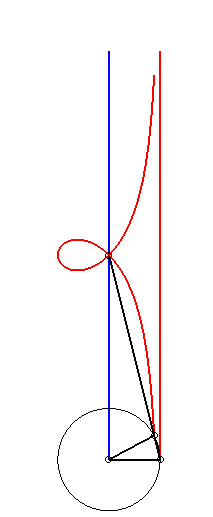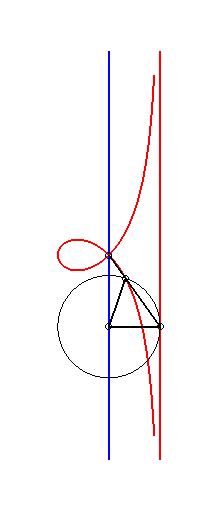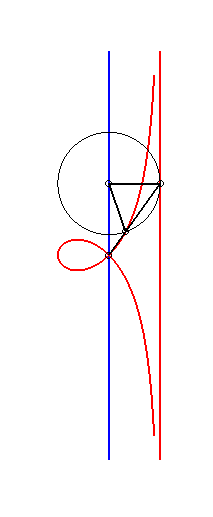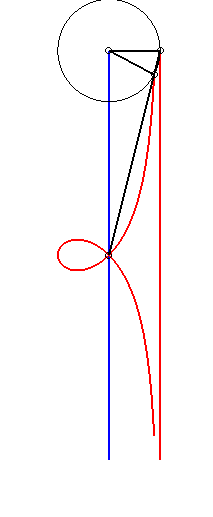
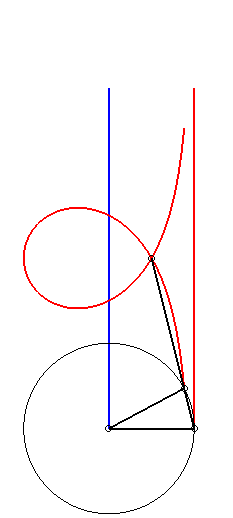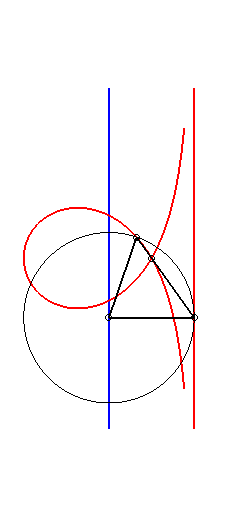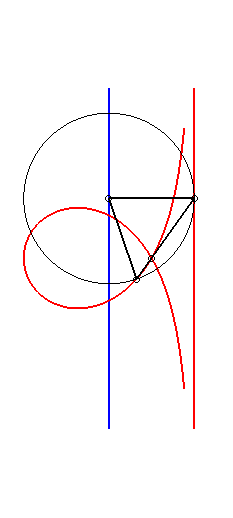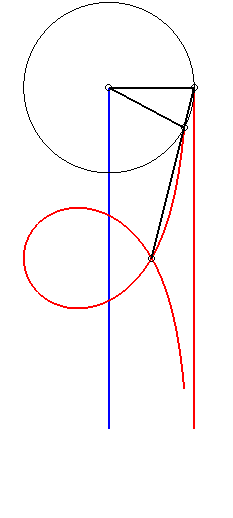
| Etant donnés deux points N et P de même ordonnée, décrivant respectivement les droites x = a et x = b, la kiéroïde est le lieu des points d'intersection du cercle de centre P et de rayon c avec la droite (ON). | 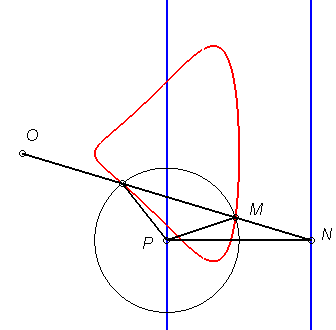 |
 |
Lorsque
(soit lorsque le cercle est tangent à la droite x = a) ,
la kiéroïde se décompose en une cubique
circulaire rationnelle droite et son asymptote x = a, et on
obtient ainsi toutes les cubiques circulaires rationnelles droites, ce
qui fournit une nouvelle construction de ces courbes.
Lorsque a = b+c, la cubique s'écrit
ou
avec
les cas particuliers :
| a = 2b = 2c : cissoïde droite | a = c, b = 0 : strophoïde droite | 2a = -2b = c : trisectrice de Mac-Laurin |
 |
 |
 |
Lorsque a = b - c, la cubique s'écrit 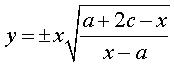 ou ou |
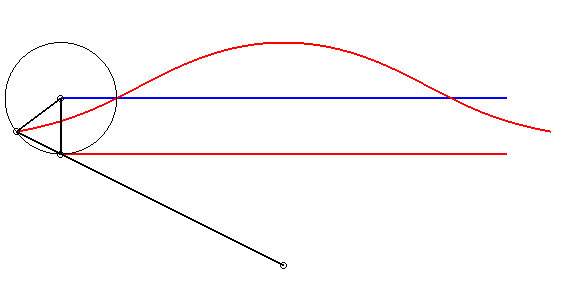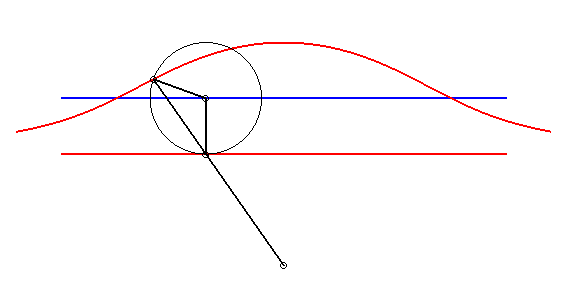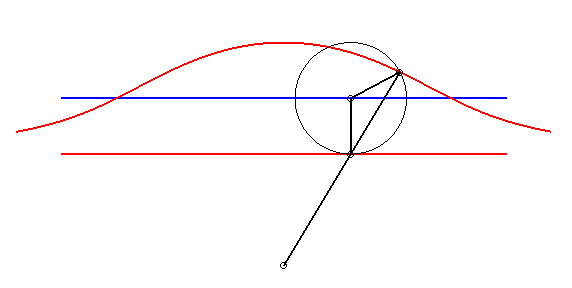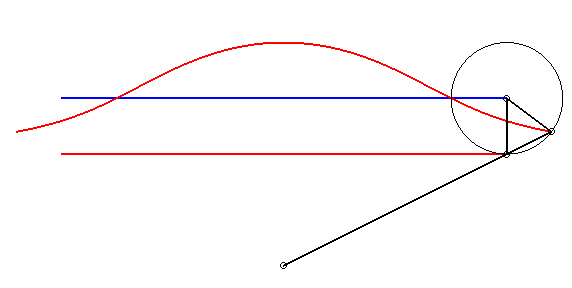 |
| Lorsque a = b, on obtient les conchoïdes
de droites :
|
Lorsque b = c, la kiéroïde présente
un rebroussement en O ; lorsque de plus a >> 2b, la
kiéroïde |
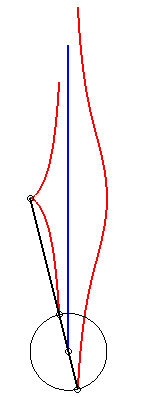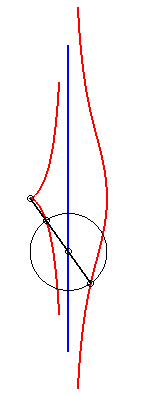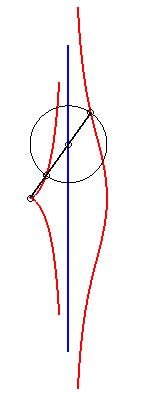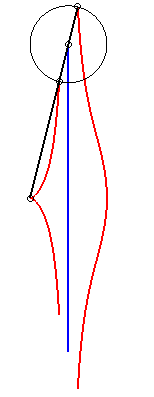 |
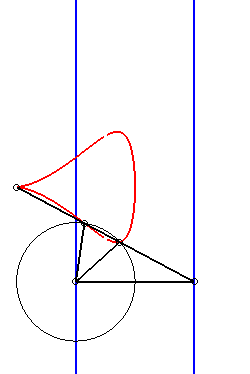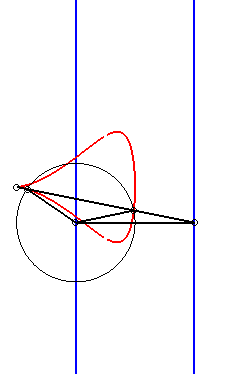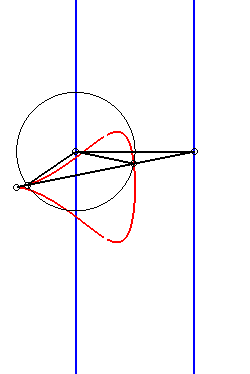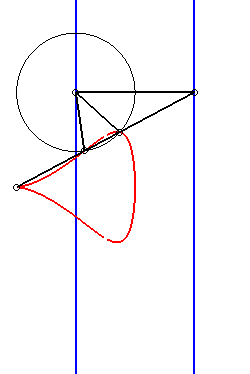 |
Comparer avec les courbes
de Rosillo.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL
2011