Couture de balle de tennis

COUTURE DE BALLE DE TENNIS
Seam line of a tennis ball, Nahtlinie des Tennisballes

Vue ci-dessus réalisée avec povray par Alain Esculier.
Site en allemand.

Quelle est la courbe suivie par la couture d'une balle de tennis ?

Il semble naturel d'imposer comme conditions à cette courbe

1) d'être tracée sur une sphère (par exemple de centre O)

2) d'être invariante par retournement

3) de séparer la sphère en deux morceaux échangés par le retournement précédent.

Une possibilité est alors la courbe réunion de 4 demi-cercles présentée ci-contre. Cette courbe est la courbe de contact de la sphère inscrite dans un sphéricône, surface formée de 4 portions de cônes de révolution.

Mais cette courbe présente des discontinuités de courbure, et on peut se demander si on peut rajouter à la courbe la propriété :

4) d'être rationnelle

La réponse est oui : la vue 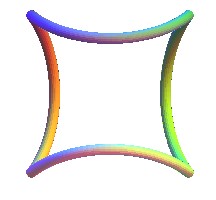donne l'idée de prendre pour projection sur xOy une hypotrochoïde à symétrie d'ordre 4 : , et avec une fonction sinusoïdale adéquate pour z, on obtient la courbe :

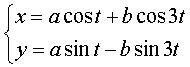
Paramétrisation cartésienne : .
Courbe tracée sur une sphère (de centre O et de rayon d = a+b) ssi .
Courbe rationnelle de degré 6.
Les 3 axes sont axes de retournement, mais seuls Ox et Oy échangent les deux parties de la sphère découpées par la courbe.

Ci-contre la déformation de la courbe, qui est un cas particulier de courbe des satellites, pour d constant et a variant de d/2 à d.
Le cas b = a = d/2 (point double au pôle nord) donne une clélie, dont la vue de dessus est un quadrifolium.
Peu après d/2, la courbe passe par une phase ressemblant à la courbe du ballon de basket (faisant abstraction des deux grands cercles tracés sur ce ballon).

La valeur de b pour laquelle la courbe a une tangente verticale au point d'intersection avec l'équateur est b = a / 3 (la projection est une astroïde). Cela correspond à peu près visuellement à la courbe réelle.
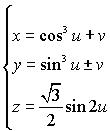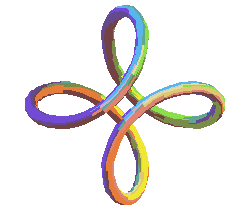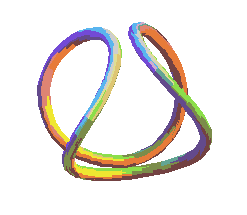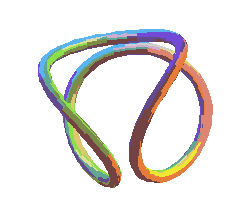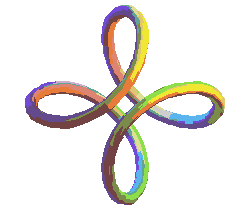Cette courbe de paramétrisation est l'intersection des deux cylindres d'axes orthogonaux :.

Diverses vues de la courbe pour b légèrement inférieur à a. Cette courbe est l'intersection de la sphère avec une surface cubique : c'est une courbe algébrique de degré 2x3 = 6.

Mais peut-on trouver une autre courbe vérifiant les propriétés 1) à 4) ?

Sur www.gebr-grimm.de/cucke/seite2.htm est dénommée "Tennisballkurve" l'intersection de la sphère avec un paraboloïde hyperbolique . Cette courbe possède l'avantage d'être de degré 4 (c'est une biquadratique sphérique), mais ne vérifie pas la propriété 4) : elle n'est pas rationnelle.
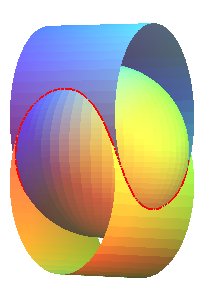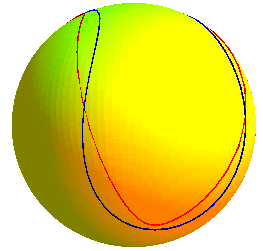
Elle est aussi l'intersection des deux cylindres elliptiques et où (voir ce site où elle est dénommée courbe de Bishop).
Cette courbe est donc une dilatation de bicylindrique.

Une autre possibilité est la sinusoïde sphérique à deux arches, intersection d'un demi cône sinusoïdal : avec une sphère.
C'est la moitié d'une courbe algébrique de degré 8.
La comparaison montre que cette courbe (en rouge) est moins harmonieuse que la courbe ci-dessus (en bleu).

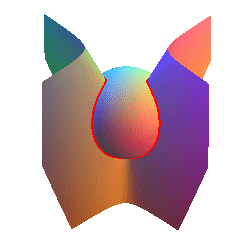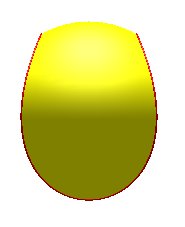
Autre possibilité : section du conoïde de Plücker avec une sphère de diamètre plus grand que la "hauteur" du conoïde ; c'est une courbe algébrique de degré 6, non rationnelle.

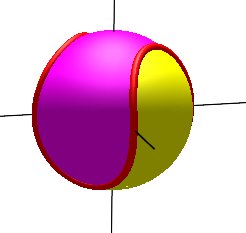
La couture partage la surface de la balle en deux parties égales, mais le cône de sommet le centre, et qui s'appuie sur cette couture, partage également l'intérieur de la balle en deux parties égales !
C'est cette idée qu'utilise le sculpteur Patrick Collandre pour développer en trois dimensions le classique symbole du yin et du yang.
Sa courbe de séparation est formée de 4 arcs de cercle.
Il a dénomé sa sculpture : sphère tao.

Mais revenons à la couture de balle de tennis comme courbe de contact entre le sphéricône et la sphère inscrite. L'enveloppe convexe de la couture est alors formée de deux portions de cylindre et 4 demi-disques : c'est le dual polaire du sphéricône par rapport à cette sphère. Tadeusz Dorozinski l'a dénommé : sphéricylindre.

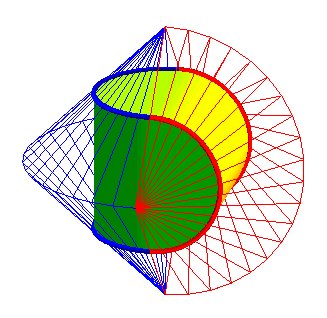Remarque : Le théorème de la balle de tennis affirme que toute courbe lisse autre qu'un cercle partageant la sphère en deux parties isométriques a au moins 4 points d'inflexion.

Voir aussi cet article sur le "base-ball cover".

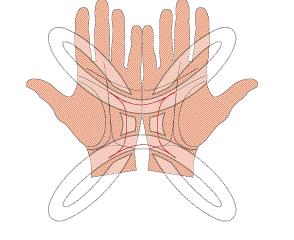Vue d'artiste d'une courbe ressemblant fort à la vue de dessus de la courbe de la balle de tennis.

Logo d'un opérateur de télécom belge

Sculpture due à Vieweger située à l'entrée d'un club de tennis à Munich.


Diverses vues de la courbe pour b légèrement inférieur à a.	Cette courbe est l'intersection de la sphère avec une surface cubique : c'est une courbe algébrique de degré 2x3 = 6.

Sur www.gebr-grimm.de/cucke/seite2.htm est dénommée "Tennisballkurve" l'intersection de la sphère avec un paraboloïde hyperbolique . Cette courbe possède l'avantage d'être de degré 4 (c'est une biquadratique sphérique), mais ne vérifie pas la propriété 4) : elle n'est pas rationnelle. Elle est aussi l'intersection des deux cylindres elliptiques et où (voir ce site où elle est dénommée courbe de Bishop). Cette courbe est donc une dilatation de bicylindrique.
Une autre possibilité est la sinusoïde sphérique à deux arches, intersection d'un demi cône sinusoïdal : avec une sphère. C'est la moitié d'une courbe algébrique de degré 8. La comparaison montre que cette courbe (en rouge) est moins harmonieuse que la courbe ci-dessus (en bleu).
Autre possibilité : section du conoïde de Plücker avec une sphère de diamètre plus grand que la "hauteur" du conoïde ; c'est une courbe algébrique de degré 6, non rationnelle.