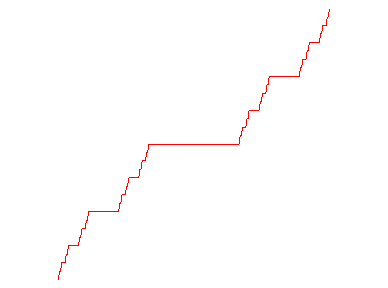
ESCALIER DU DIABLE
Devil's staircase, Teufelstreppe
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ESCALIER DU DIABLE
Devil's staircase, Teufelstreppe

| Courbe découverte par Ludwig Scheeffer, élève
de Cantor, en 1885.
La courbe de Bolzano-Lebesgue avait été découverte en 1830 par Bolzano, mais non publiée. Autres noms : courbe, ou escalier de Cantor-Lebesgue. Références historiques : ce lien. |
| Équation cartésienne : y = f(x)
où la fonction f est définie sur [0, 1] comme suit
: si le développement ternaire impropre de x ne comporte
que des 0 ou des 2 (c'est-à-dire, si x appartient à
l'ensemble de Cantor), alors f(x)
est le nombre obtenu en changeant les chiffres 2 en des chiffres 1, nombre
lu en base 2.
Si le développement ternaire de x contient un 1, alors f(x) = f(x'), x' étant le nombre obtenu en tronquant x après le premier 1 rencontré. |
Code Maple :
escalier:=proc(a,b,c,d,n) local liste; if n=0 then liste:=[a,b],[c,d] else liste:= escalier(a, b, (2*a+c)/3, (b+d)/2, n-1), escalier((2*a+c)/3, (b+d)/2, (a+2*c)/3, (b+d)/2, n-1), escalier((a+2*c)/3, (b+d)/2, c, d, n-1) fi; liste end: plot([escalier(0,0,1,1,3)]); |
On note E l'espace des fonctions continues f réelles sur [0,1], telles que f(0) = 0 et f(1) = 1, et T l'opérateur défini sur E par :
On montre aisément que T est une contraction de E, qui est complet pour la norme de la convergence uniforme ; T admet donc un point fixe, appelée fonction de Cantor-Lebesgue. L'escalier du diable est la courbe de cette fonction.
Cette fonction a été construite pour donner un exemple de fonction continue ayant une dérivée nulle presque partout (sur le complémentaire de l'ensemble de Cantor) et qui n'est cependant pas constante ; autrement dit, l'escalier du diable est ainsi nommé car il est continu, a presque partout une tangente horizontale, et pourtant il monte ! Inversement bien sur, la tangente est verticale en tout point dont l'abscisse appartient à l'ensemble de Cantor.
Si l'on part de f0(x) = x, la fonction fn = Tn(f) est l'unique fonction de E qui est constante sur chacun des intervalles constituant le complémentaire de l'ensemble de Cantor à l'étape n , noté Cn, et affine de pente (3/2)n sur chacun des intervalles de Cn.
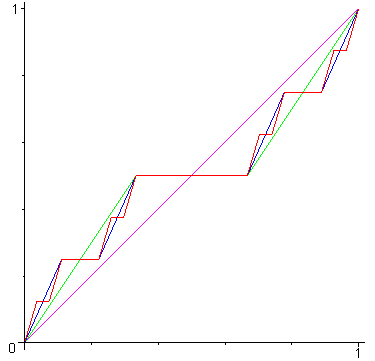
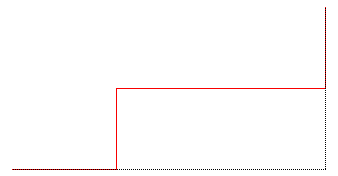
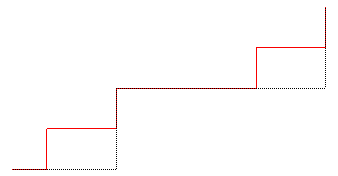
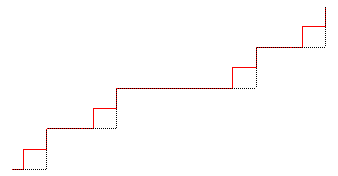
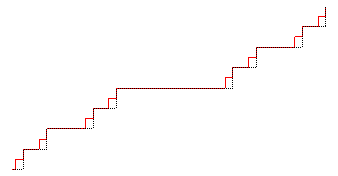
L'escalier du diable est aussi l'attracteur
des trois contractions affines F, G, H définies
par .
Le n-ième compact associé à cette famille de
contractions, en partant du segment [(0,0) (1,1)] n'est autre que la courbe
de la fonction fn.
Généralisation :
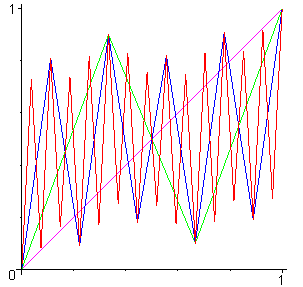
Si pour t dans ]0,1[, on considère les
trois contractions Ft , Gt
,
Ht
définies par :
,
on obtient un attracteur qui est l'escalier du diable pour t = 1/2,
et la courbe de Bolzano-Lebesgue pour t = 2/3.
La généralisation de la contraction T
ci-dessus est Tt,
définie par :
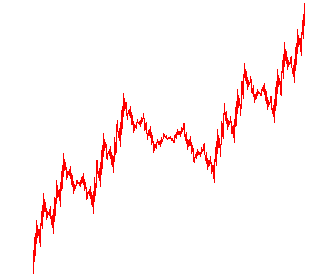
Le point fixe ft
de Tt a
la propriété remarquable d'être une fonction continue
nulle-part dérivable pour t > 1/2.
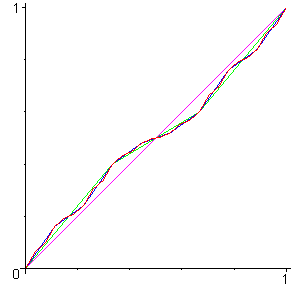
|
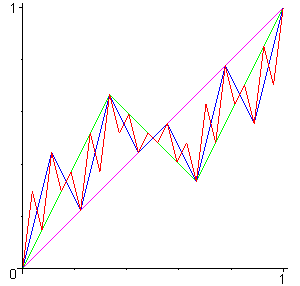
|
|
 |
Code Maple :
escalier:=proc(a,b,c,d,t,n) local liste; if n=0 then liste:=[a,b],[c,d] else liste:= escalier(a, b, (2*a+c)/3, (1-t)*b+t*d, t, n-1), escalier((2*a+c)/3, (1-t)*b+t*d, (a+2*c)/3, t*b+(1-t)*d, t, n-1), escalier((a+2*c)/3, t*b+(1-t)*d, c, d, t, n-1) fi; liste end: plot([escalier(0,0,1,1,2/3,3)]); |
Comparer avec la courbe du blanc-manger.
Voir aussi la courbe
de Lebesgue, courbe définie à partir de la fonction de
Cantor-Lebesgue.
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2019