ENSEMBLE UNITÉ
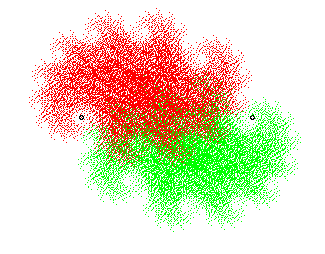
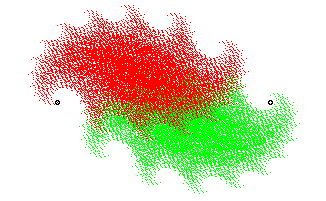
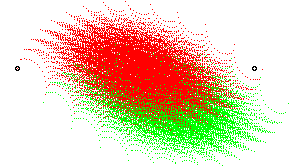
En rouge et vert les deux parties semblables au tout ; les deux points
sont les centres des deux similitudes.
Télécharger un logiciel de tracé en temps réel de ces fractals, dû à Arnaud Chéritat.
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ENSEMBLE UNITÉ



En rouge et vert les deux parties semblables au tout ; les deux points
sont les centres des deux similitudes.
Télécharger un logiciel de tracé en temps réel de ces fractals, dû à Arnaud Chéritat.
| Notion étudiée par Barnsley et Harrington en 1985 et Goffinet en 1991. |
Étant donné un complexe b, l'ensemble unité Ub associé est l'adhérence de l'ensemble des sommes finies des puissances entières naturelles de b :
.
Lorsque b est de module strictement inférieur à 1, Ub est alors l'ensemble des sommes finies ou infinies des puissances entières naturelle de b :
D'ailleurs Ub
est :
- soit totalement discontinu si f1
(Ub)
et f2 (Ub)
sont disjoints (coloriés en rouge et vert dans les figures).
- soit connexe si f1
(Ub)
et f2 (Ub)
se coupent.
Par analogie avec l'ensemble de Mandelbrot classique (qui est l'ensemble des complexes c tels que l'ensemble de Julia Jc soit connexe), on désigne aussi par ensemble de Mandelbrot l'ensemble des b tels que Ub soit connexe.
Cet ensemble a une frontière fractale qui est incluse, d'après ce qui précède, dans l'anneau 1/Ö2 £ |b| £ 1/ 2.
Quelques cas particuliers :
| b | Ub |
| 1 ou 2 | N |
| entier ³ 2 | entiers s'écrivant avec des 0 ou des 1 en base b |
| 1/2 | [0,2] |
| 1/3 | ensemble de Cantor d'extrémités 0 et 3/2 |
| 1/n avec n entier >1 | réels de [0, n/(n -1)] sécrivant en base n avec des 0 ou des 1. |
| (1+i)/2 | dragon symétrique |
| exp(ip/3) | réseau triangulaire |
| i | réseau carré |
Ci-dessous quelques exemples avec indication de la valeur
de b, du rapport de similitude r, de l'angle a et
de la dimension de similitude d (en valeurs approchées) ;
les noms de baptème sont ceux donnés par Daniel Goffinet.
Les parties A utilisées ont 16 éléments au
maximum et le dessin ne représente donc qu'une partie de l'ensemble
unité complet, principalement quand r est proche de 1.

Le rucher s'effiloche : b = 0,49+0,84i ; r = 0,97 ; a = 60° ; d = 23. |
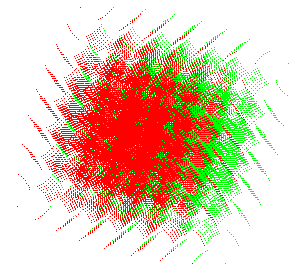
Set de table : b = 0,04+0,97i ; r = 0,97 ; a = 88° ; d = 23. |
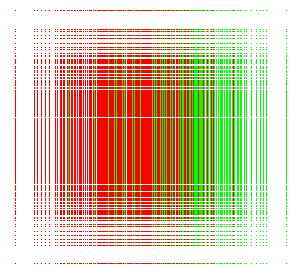
Tartan skirt : b = 0,93i ; r = 0,93 ; a = 90° ; d = 10. |
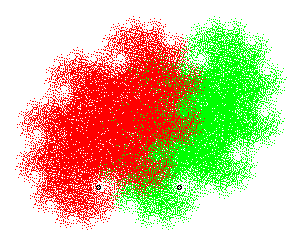
Olé : b = 0,7+0,39i ; r = 0,8 ; a = 30° ; d = 3. |

Dragon symétrisé : b = 0,5+0,5i ; r = 0,71 ; a = 45° ; d = 2. |

Dragon mité : b = 0,65+0,3i ; r = 0,72 ; a = 25° ; d = 2. |

Chou-fleur : b = 0,4+0,6i ; r = 0,72 ; a = 56° ; d = 2. |
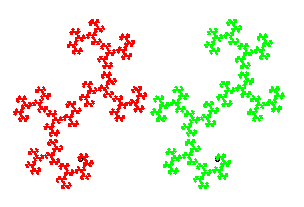
Danse macabre : b = 0,39+0,49i ; r = 0,62 ; a = 51° ; d = 1,4. |
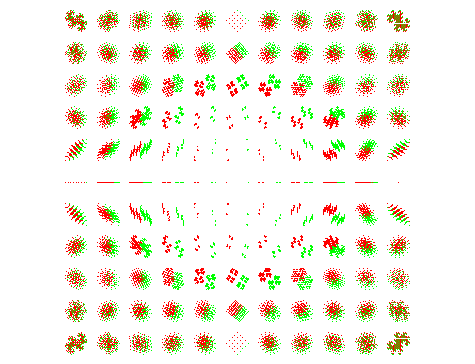
|
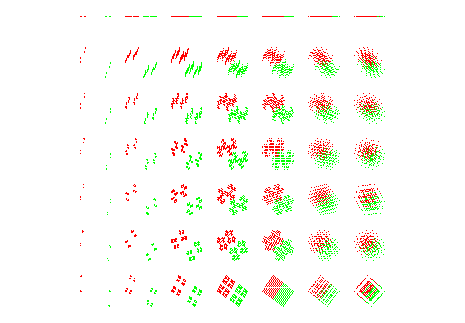
Les fractals sont ici rangés de gauche à droite par rapport de similitude croissant de 0.1 à 0.9 (donc dimension croissante) et de haut en bas par angle de similitude croissant de 0 à 90°. |
| fractal suivant | fractal précédent | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2001