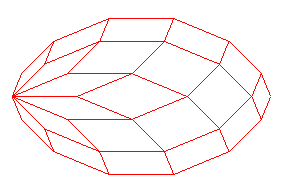
Si l'on contracte successivement (dans un ordre quelconque) ces p parallélogrammes, on obtient une succession de zonogones emboîtés dont le dernier est un point (voir ci-contre).
Inversement, tout zonogone plein est donc obtenu en partant d'un point par étirements successifs dans p directions différentes.
Autrement dit, les zonogones pleins à 2p sommets sont les sommes de Minkowski de p segments (non deux à deux parallèles) du plan, que nous désignerons par p-zonogone.
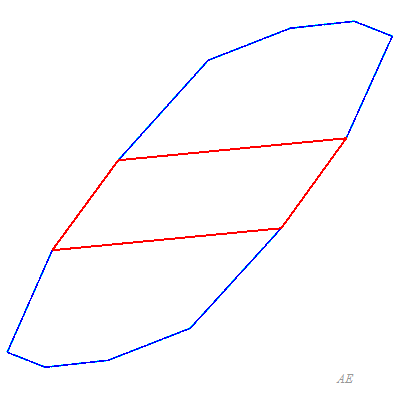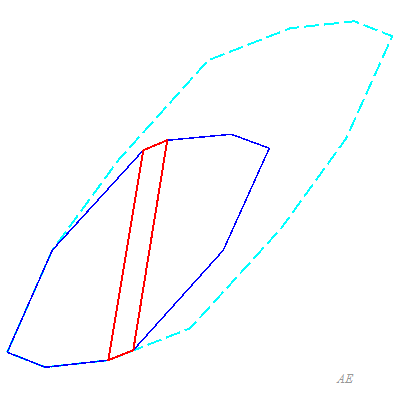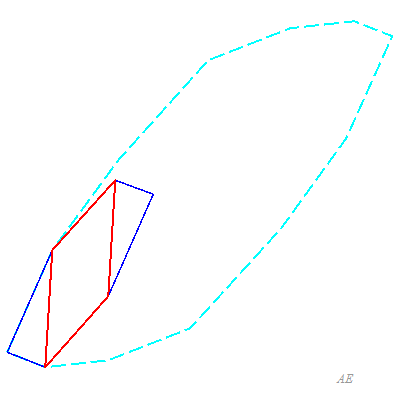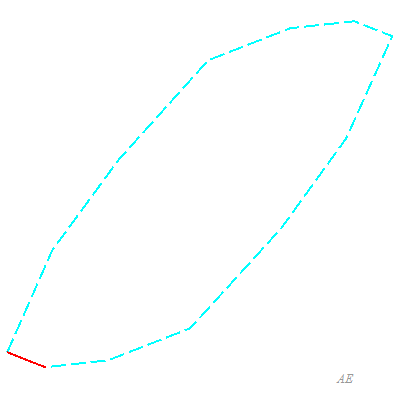
Ceci vient de ce que tout p-zonogone plein est obtenu par translation d'un p–1-zonogone plein à 2(p–1) côtés, faisant apparaître p–1 nouveaux parallélogrammes.
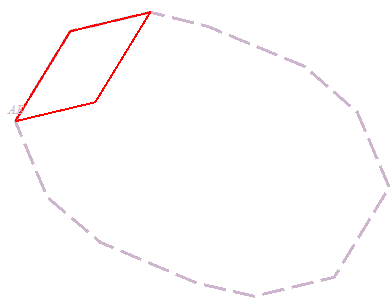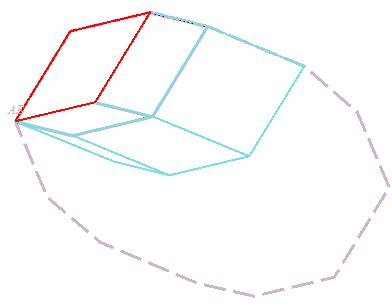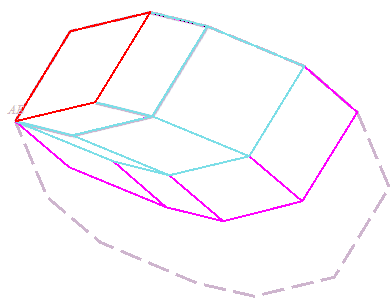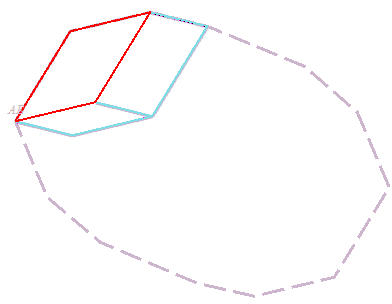
En particulier, tout polygone régulier à n = 2p côtés se décompose en n(n–2)/8 losanges ; voir à rosace rhombique une autre méthode pour obtenir cette dissection.
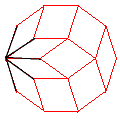
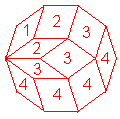
Le zonogone est alors recouvert par p zones (d'où son nom), joignant chaque côté au côté symétrique, formées chacunes des p–1 parallélogrammes dont deux côtés ont une direction donnée. Chaque parallélogramme est traversé par deux zones.
On peut étirer où contracter des zones (de sorte par exemple à rendre le zonogone équilatéral).
La contraction complète d'une zone donne un p–1 zonogone.
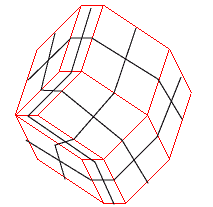
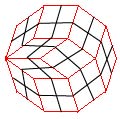
Deux 5-zonogones, l'un irrégulier, l'autre régulier, ayant 2p=10 côtés, pavés par p(p-1)/2=10 parallélogrmmes, formant p=5 zones formées chacune de p-1=4 parallélogrammes.